A logic puzzle by MIT mathematician Tanya Khovanova: You’re visiting an island on which every resident is either a knight or a knave. Knights always tell the truth, and knaves always lie. All the islanders know one another. You meet three islanders, Alice, Bob, and Charlie, and ask each one, “Of the two other islanders here, how many are knights?” Alice says, “Zero.” Bob says, “One.” What will Charlie say?

A prizewinning problem by Paul Bekkelund from the Norwegian chess magazine Sjakk-Nytt, 1947. White to mate in two moves.

A problem proposed by Ashay Burungale of Satara, Maharashtra, India, in the November 2008 issue of American Mathematical Monthly: In a certain town of population 2n + 1, all relations are reciprocal: If Person 1 knows Person 2, then Person 2 knows Person 1. For any set A that consists of n citizens, there’s some person among the remaining n + 1 who knows everyone in A. Prove that there’s some citizen of the town who knows all the others.

Each of three people is wearing either a red hat or a blue hat. Each can see the color of the others’ hats but not her own. Each is told to raise her hand if she sees a red hat on another player. The first to guess the color of her own hat correctly wins.

All three raise their hands. A few minutes pass in which no guesses are made, and then one player says “Red” and wins. How did she know the color of her hat?

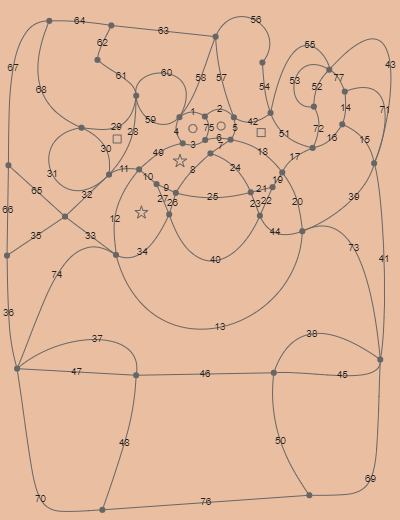
Matthew Scroggs has released this year’s Christmas card for Chalkdust magazine.

This year’s card contains nine mathematical puzzles. Finding the right answers will reveal a Christmas-themed picture in the image above.

You can download the card as a PDF or complete it online.

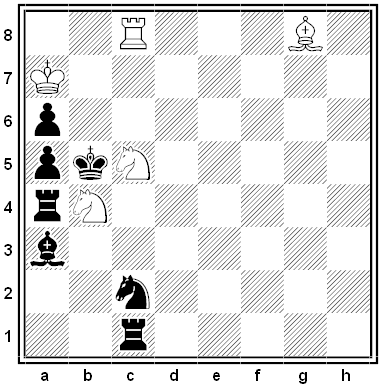
A “grid-chess” problem by E. Visserman, from Fairy Chess Review, 1954. A grid divides the board into 16 large squares, and each move by each side must cross at least one line of the grid. For example, in this position it would be illegal for the black king to move to f3. How can White mate in two moves?

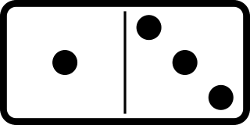
A problem proposed by C. Gebhardt in the Fall 1966 issue of Pi Mu Epsilon Journal:

A particular set of dominoes has 21 tiles: (1, 1), (1, 2), … (1, 6), (2, 2), … (6,6). Is it possible to lay all 21 tiles in a line so that each adjacent pair of tile ends matches (that is, each 1 abuts a 1, and so on)?

At a Mensa gathering in 2003, Robert Abbott tried out a new type of maze — five bureaucrats sit at desks, and solvers carry forms among them:

When you enter the maze you are given a form that says, ‘Take this to the desk labeled Human Resources.’ You look for the desk with the nameplate Human Resources, you hand in your form to the bureaucrat at that desk, and he gives you another form. This one says, ‘Take this form to Information Management or Marketing.’ Hmm, there is now a choice. Let’s say you decide to go to Information Management. You hand in your form and receive one that says, ‘Take this form to Employee Benefits or Marketing.’ You decide on Employee Benefits where you receive a form saying, ‘Take this form to Corporate Compliance or Human Resources.’

Of the 30 participants, half gave up fairly soon, but the rest kept going until they’d solved it, taking 45 minutes on average. Here’s an online version with four desks, and here’s a fuller description of the project and its variants, including a Kafkaesque 2005 version by Wei-Hwa Huang in which the participants don’t know they’re in a maze.

More of Abbott’s logic mazes.