
A puzzle by Joseph Horton, from MIT Technology Review, January-February 1999:
If the sun takes two minutes to set, what angle does it subtend from Earth?

A puzzle by Joseph Horton, from MIT Technology Review, January-February 1999:
If the sun takes two minutes to set, what angle does it subtend from Earth?
Eureka, the esteemed journal of recreational mathematics published at Cambridge University, has placed its archives online under a Creative Commons license. Here’s a problem from May 1940:
The chicken was twice as old when when the day before yesterday was to-morrow to-day was as far from Sunday as to-day will be when the day after to-morrow is yesterday as it was when when to-morrow will be to-day when the day before yesterday is to-morrow yesterday will be as far from Thursday as yesterday was when to-morrow was to-day when the day after to-morrow was yesterday. On what day was the chicken hatched out?
This impressive puzzle appeared recently in the Magpie, a magazine for advanced UK-style cryptic puzzles. See the file for instructions.
A problem from the Sixth International Mathematical Olympiad, 1964: Seventeen people correspond by mail, each with all the rest. They discuss only three topics, and each pair of correspondents addresses only one of these. Prove that there are at least three people who write to each other about the same topic.

A curious chess problem from the Jamaica Gleaner. White has just moved. If he retracts this move, he can play another that forces Black to checkmate White immediately. What move does he retract?

Here are eight new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
King William’s College, on the Isle of Man, has posted the 2020 edition of “The World’s Most Difficult Quiz,” with its customary epigraph, Scire ubi aliquid invenire possis ea demum maxima pars eruditionis est (“The greatest part of knowledge is knowing where to find something”). Answers will be posted on January 20; as usual, MetaFilter is maintaining a Google spreadsheet of communal guesses.
And the Royal Statistical Society has posted its own 2020 Christmas quiz, which it describes as “brain-melting.” “You’ll need a combination of general knowledge, logic, and lateral thinking skills to successfully crack these puzzles — but as always, no specialist mathematical knowledge is required.” Solutions are due by the end of January; the top prize is £150 in Wiley book vouchers.
William Friedman, the father of modern American cryptology, was fond of a cipher devised by Francis Bacon — a scheme so flexible that it could hide a message in a drawing, a piece of sheet music, almost any imaginable setting (“anything can be made to signify anything”).
In 1918 he used it to hide a message in the graduation photograph of the codebreakers’ class that he’d taught with his wife Elizebeth (click to enlarge). Some students are looking at the camera, others to the side — they’re encoding the message KNOWLEDGE IS POWER, a quotation of Bacon’s that was a favorite of Friedman’s.
Friedman kept the photo on his desk for the rest of his career, and when he died in 1969 Elizabeth had the phrase engraved on his tombstone, in a design of her own devising:
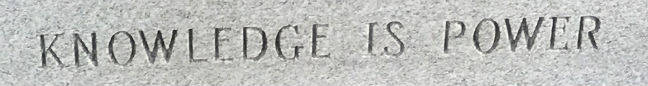
In 2017, cryptographer Elonka Dunin noticed that the inscription is composed of both serif and sans-serif letters. It turns out that even this is a cipher — Elizabeth had used it to conceal the letters WFF, William’s initials. Dunin calls it “a fitting tribute, in the life of a couple who had been so dedicated to the field of codes and ciphers.”
There’s more on the Friedmans’ legacy in this NSA publication.