Puzzles
Quickie
CHAIN is to INGOT as MILLS is to … ?
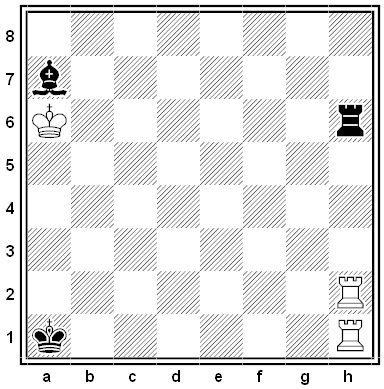
The Substitute
Between July 2015 and October 2018, the National Security Agency offered a monthly puzzle written by a staff member. Here’s the puzzle for October 2015, created by applied research mathematician Ben E.:
Kurt, a math professor, has to leave for a conference. At the airport, he realizes he forgot to find a substitute for the class he was teaching today! Before shutting his computer off for the flight, he sends an email: “Can one of you cover my class today? I’ll bake a pie for whomever can do it.” He sends the email to Julia, Michael, and Mary Ellen, his three closest friends in the math department, and boards the plane.
As Kurt is well-known for his delicious pies, Julia, Michael, and Mary Ellen are each eager to substitute for him. Julia, as department chair, knows which class Kurt had to teach, but she doesn’t know the time or building. Michael plays racquetball with Kurt so he knows what time Kurt teaches, but not the class or building. Mary Ellen helped Kurt secure a special projector for his class, so she knows what building Kurt’s class is in, but not the actual class or the time.
Julia, Michael, and Mary Ellen get together to figure out which class it is, and they all agree that the first person to figure out which class it is gets to teach it (and get Kurt’s pie). Unfortunately the college’s servers are down, so Julia brings a master list of all math classes taught that day. After crossing off each of their own classes, they are left with the following possibilities:
- Calc 1 at 9 in North Hall
- Calc 2 at noon in West Hall
- Calc 1 at 3 in West Hall
- Calc 1 at 10 in East Hall
- Calc 2 at 10 in North Hall
- Calc 1 at 10 in South Hall
- Calc 1 at 10 in North Hall
- Calc 2 at 11 in East Hall
- Calc 3 at noon in West Hall
- Calc 2 at noon in South Hall
After looking the list over, Julia says, “Does anyone know which class it is?” Michael and Mary Ellen immediately respond, “Well, you don’t.” Julia asks, “Do you?” Michael and Mary Ellen both shake their heads. Julia then smiles and says, “I do now. I hope he bakes me a chocolate peanut butter pie.”
Which class does Kurt need a substitute for?
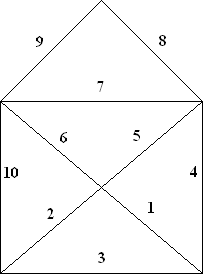
Quarters

USC mathematician Solomon Golomb offered this puzzle in his column, “Golomb’s Gambits,” in Johns Hopkins Magazine. How can you dissect this figure into four congruent pieces?
After You
A problem from Canada’s 2003 Hypatia contest:
Xavier and Yolanda are playing a game. They begin with two piles of three coins each and take turns; on each turn a player removes one or more coins from any one pile. The winner is the player who takes the very last coin. Xavier always goes first, but Yolanda has a strategy that ensures that she will always win. What is it?
A Christmas Puzzle

University of Cambridge mathematician Matthew Scroggs has post his annual Christmas puzzle: Behind each day in an advent calendar lies a puzzle with a three-digit answer. Combined, the answers reveal a series of compass directions that lead to Santa’s house. Ten randomly selected people who solve all the puzzles and find Santa’s house will receive prizes. More info here.
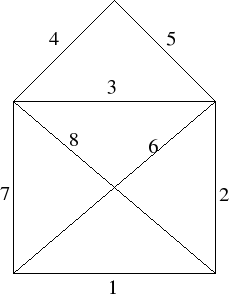
The Logic House
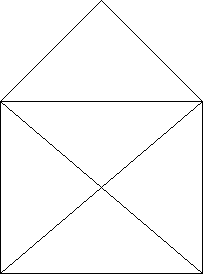
Can you draw this figure without lifting your pencil from the paper?
Foursquare
A puzzle proposed by David L. Silverman in the Fall 1963 issue of Pi Mu Epsilon Journal:
The points of the plane are divided into two sets. Prove that at least one set contains the vertices of a rectangle.
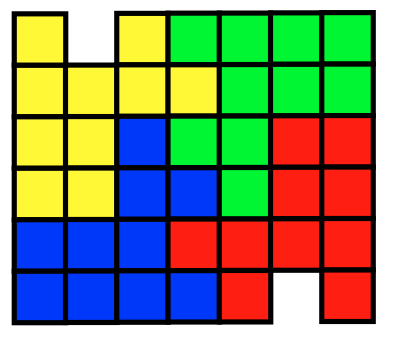
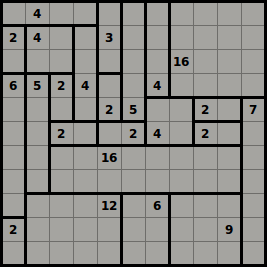
Shikaku

Japanese publisher Nikoli produces this geometric logic puzzle. Can you divide this grid into rectangular and square pieces such that each piece contains exactly one number and each number reflects its piece’s area?