Puzzles
Another First
Jules Verne’s 1882 novel La Jangada tells the story of Joam Dacosta, a Brazilian man wrongly accused of theft and murder. In Book Two his friends struggle to save him by solving a cryptogram, whose last paragraph is given in the text:
Phyjslyddqfdzxgasgzzqqehxgkfndrxujugiocytdxvksbxhhuypo
hdvyrymhuhpuydkjoxphetozsletnpmvffovpdpajxhyynojyggayme
qynfuqlnmvlyfgsuzmqiztlbqgyugsqeubvnrcredgruzblrmxyuhqhp
zdrrgcrohepqxufivvrplphonthvddqfhqsntzhhhnfepmqkyuuexktog
zgkyuumfvijdqdpzjqsykrplxhxqrymvklohhhotozvdksppsuvjhd.
In the end this works out to:
Le véritable auteur du vol des diamants et de l’assassinat des soldats qui escortaient le convoi, commis dans la nuit du vingt-deux janvier mil huit cent vingt-six, n’est donc pas Joam Dacosta, injustement condamné à mort; c’est moi, le misérable employé de l’administration du district diamantin; oui, moi seul, qui signe de mon vrai nom, Ortega.
In the article linked below, Miami University mathematician Frederick Gass explains rigorously how the cipher might be solved. In the novel, Judge Jarriquez has a brainstorm: He learns that the writer might have been named Ortega, guesses that the declaration might end with that signature, and works out the rest from there.
“By virtue of this solution, Jules Verne is credited with the first published exposition of the probable word method for Gronsfeld ciphers.”
(Frederick Gass, “Solving a Jules Verne Cryptogram,” Mathematics Magazine 59:1 [February 1986], 3-11.)
The Hard Way
This is great — Eugene Wigner tells the story of Max Born giving the “two bikes and a fly” puzzle to John von Neumann (it starts at 16:50).
(Via Tamás Görbe, from an old VHS video digitized by Robert Klips.)
A Captivating Entertainment
Visitors to La Granja, Philip V’s retreat overlooking Madrid, may have found this unusual labyrinth a bit too involving. It’s a “vortex maze”: It “leads you directly to the centre, but its spiralling options for exit are your undoing,” explain Angus Hyland and Kendra Wilson in The Maze: A Labyrinthine Compendium (2018). “On paper, it is a beautiful design, and in reality it is almost twice as large as the ‘record-breaking’ maze at Longleat, made 250 years later.”
Philip’s French landscapers drew it from La théorie et la pratique du jardinage, the best-selling gardening manual published by Antoine Joseph Dezallier d’Argenville in 1709.
The Church Cipher
In 1775, an enciphered message was intercepted en route from colonial physician Benjamin Church to a British officer in Boston. Part of the message appears below. What does it say?
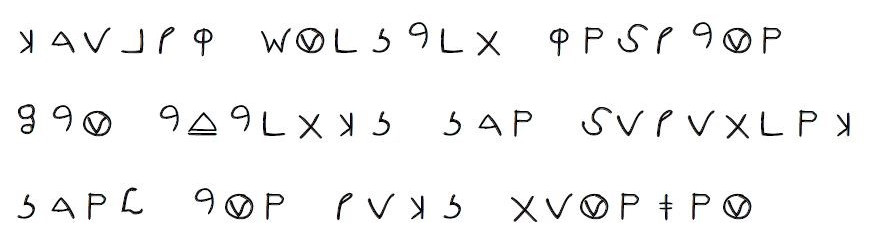
Black and White

Physicist Roger Penrose devised this problem in 2017 to illustrate the difference between artificial and human intelligence. James Tagg, leader of the Penrose Institute, told the Telegraph, “A human looking at it for a short while will ‘see’ what white must, and more particularly, must not do, and use very little energy to decide this. But, for a computer, the puzzle requires an enormous number of calculations, far too many for even today’s supercomputers.” What is White’s insight?
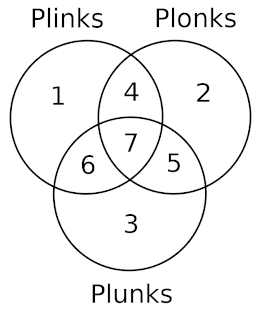
Euphony
A charming puzzle from Crux Mathematicorum, December 2004:
If all plinks are plonks and some plunks are plinks, which of these statements must be true?
X: All plinks are plunks.
Y: Some plonks are plunks.
Z: Some plinks are not plunks.
Podcast Episode 317: Lateral Thinking Puzzles

Here are six new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
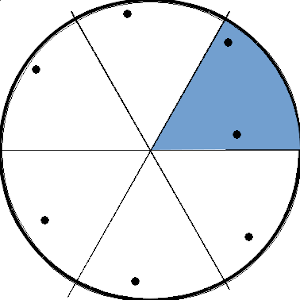
Board Meeting
Prove that if seven darts land on a dartboard, there will always be two darts that are no farther apart than the distance of one radius.
Black and White

Black is clearly lost. But there are two squares on which his king can never be checkmated, even if White is allowed to make consecutive moves and checks are ignored. What are they?