Areas from r/blackmagicfuckery
Puzzles
Black and White
Take 5
An interesting problem from Crux Mathematicorum, March 2004: The increasing sequence 1, 5, 6, 25, 26, 30, 31, 125, 126, … consists of positive integers that can be formed by adding distinct powers of 5. That is, 1 = 50, 5 = 51, 6 = 50 + 51, and so on. What’s the 75th integer in this sequence?
Black and White
The Grand Tour
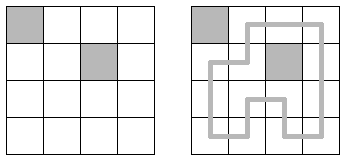
Puzzle maven Nob Yoshigahara offered this puzzle in the September-October 2000 issue of MIT Technology Review, attributing it to a Professor Kotani. In the 4 × 4 complex of rooms above, two of the rooms are closed. This leaves a single way to tour the remaining rooms in a series of orthogonal moves, visiting each room once and returning to the starting point.
The 12 × 12 complex below has a similarly unique solution. What is it?

Black and White

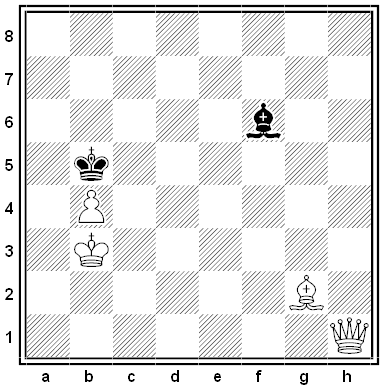
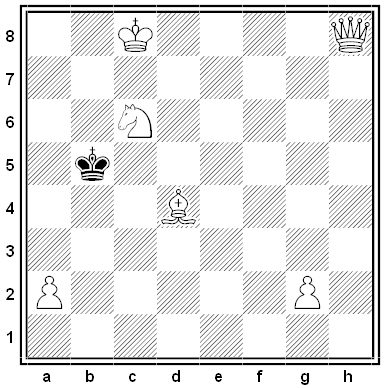
Luigi Ceriani published this curiously ambivalent retrograde puzzle in Europe Echecs in 1960. White is to mate in two moves.
The answer turns on whether White can castle kingside and whether Black can castle queenside. Castling is always deemed to be legal unless it can be proven otherwise. The question of White’s castling comes down to the origin of the rook on a6. If that started on h1, then White may not castle because the rook that’s currently on h1 obviously must have moved in order to get there. If the rook on a6 started on a1, then again White may not castle, because in that case the rook must have got to its present position via e1, since the pawn originally on a2 can have reached its present position on b3 only after the knight on a1 had itself moved there from b3.
That means that if the rook on a6 is not a promoted piece, White cannot castle. If it is a promoted piece, then Black cannot castle, because the white pawn that was promoted must have passed over either d7 or f7 first, which would have forced the black king to move if it had been on its original square. Hence either castling by White or castling by Black is impossible.
Well, if castling by Black is impossible, then White can win by castling himself, since then Black has no escape from 2. Rf8#. And if castling by White is impossible, then White can capture the b5 pawn en passant (followed by mate with the queen), because if Black’s king and rook have not moved then Black’s last move must have been b7-b5. (His last move cannot have been b6-b5 because that would leave White no possible previous move. As it is, with Black’s last move being b7-b5, White’s preceding move must have been R[c6]xa6+.)
(Via John M. Rice, An ABC of Chess Problems, 1970.) (Maybe I’m being obtuse, but isn’t it possible that neither side can castle? In that case both proposed mates fall apart and I don’t see how White can succeed.)
02/03/2020 UPDATE: Ach, I’d just given the answer to my own question: Castling is deemed to be legal unless it can be proven otherwise, and it can’t be proven that neither side can castle. (Thanks, David and Daniel.)
Genealogy
Reader Jack McLachlan found this curious entry among the marriage notices in the Scots Magazine of January 1790:
At Newburn, near Newcastle, Mr William Dormand, to Miss Hannah Hoy, of that place. The ceremony was attended by the father, mother, brother, sister, aunt, nephew, two husbands, and two wives, and yet there were only four persons present at the marriage.
No explanation is given. How is such an arrangement possible?
Parenthood
We want to line up our six children for a photograph, but we can’t put Sally and John next to one another because they fight. In how many ways can we arrange the photo with this constraint?
Black and White
The Smithy Code
In deciding a plagiarism case against author Dan Brown in 2006, British justice Peter Smith handed down a peculiar judgment: Certain letters in the text had been italicized with no explanation. Apparently inspired by Brown’s book The Da Vinci Code, Smith had hidden a message in the text.
The judgment included the sentence “The key to solving the conundrum posed by this judgment is in reading HBHG and DVC.” In context, those abbreviations refer to The Holy Blood and the Holy Grail, the book that Brown had been accused of plagiarizing, and The Da Vinci Code.
“I can’t discuss the judgement, but I don’t see why a judgement should not be a matter of fun,” Smith had said in handing down the opinion, which found Brown not guilty. He promised to confirm any correct solution.
He offered enough hints to reporters that Guardian media journalist Daniel Tench eventually solved it: It was a polyalphabetic cipher using a keyword based on the Fibonacci sequence, yielding the plaintext “Jackie Fisher who are you? Dreadnought.” Jackie Fisher was a British admiral whom Smith admired. (The code is described here; Tench describes the solving here.)
The Court of Appeal later said that Smith “was prompted by the extensive use in [The Da Vinci Code] of codes, and no doubt by his own interest in such things, to incorporate a coded message in his judgment, on which nothing turns. The judgment is not easy to read or to understand. It might have been preferable for him to have allowed himself more time for the preparation, checking and revision of the judgment.”