Puzzles
Podcast Episode 266: Lateral Thinking Puzzles

Here are seven new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
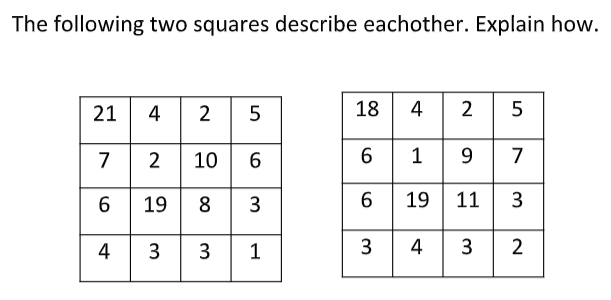
The Two Squares Puzzle
Lee Sallows just sent me this — the puzzle is difficult, but the solution is stunning:
Query
What’s remarkable about this set of words?
BIOLOGY DEATHLY SLOSHED BASTARD SELVAGE FISSILE DALLIES FLAVORS
Keeping Distance
For which values of n can n points be placed on a sphere so that all of them are equidistant from each other?
Some Two
Given 52 integers, prove that it’s always possible to find some two of them whose sum or difference is evenly divisible by 100.
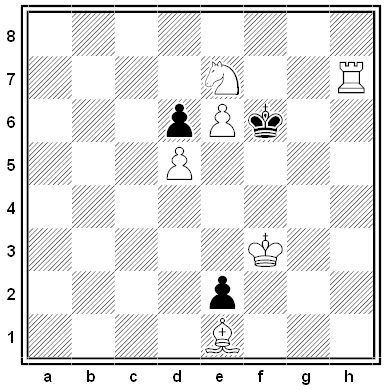
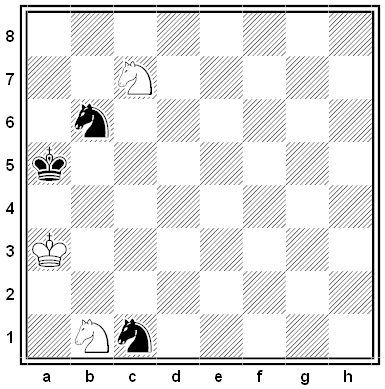
Black and White
Black and White

A remarkable thematic chess puzzle by Bodo Van Dehn, 1951. White to move and win.
The solution is 10 moves long, but all Black’s moves are forced. (That’s a very valuable hint.)
A Flea’s Journey
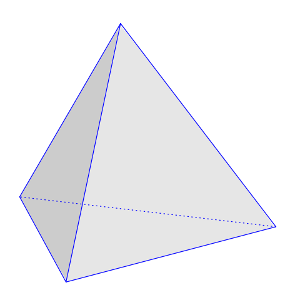
A flea sits on one vertex of a regular tetrahedron. He hops continually from one vertex to another, resting for a minute between hops and choosing vertices without bias. Prove that, counting the first hop, we’d expect him to return to his starting point after four hops.
The Magic Total
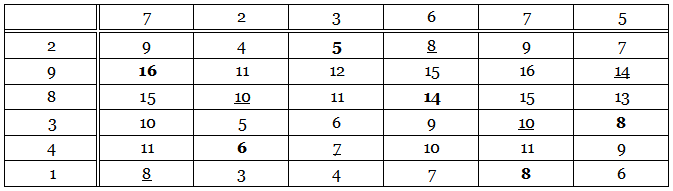
Each of the 36 numbers in this table is the sum of the numbers at the head of its column and at the left of its row. For example, 3 = 2 + 1 and 13 = 5 + 8. The six bold numbers have been chosen so that each of them falls in a different row and a different column. The underlined numbers were chosen in the same way. But each of these two sextets produces the same total: 16 + 6 + 5 + 14 + 8 + 8 = 8 + 10 + 7 + 8 + 10 + 14 = 57. In fact, any six numbers chosen in this way will produce the total 57. Why is this?