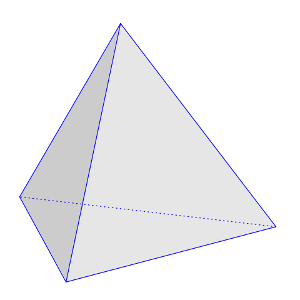
For which values of n can n points be placed on a sphere so that all of them are equidistant from each other?
| SelectClick for Answer | |
|---|---|
Roy Sinclair posed this question in the November-December 2000 issue of MIT Technology Review. Bruce Layton offered a solution in the May 2001 issue: The values are 1, 2, 3, and 4. For n = 1 there are no distances to be unequal, and for n = 2 there’s only one distance, with nothing to be unequal to. The cases of n = 3 and n = 4 can be shown by choosing two points on the sphere’s surface and centering on each of them a sphere whose radius is the distance between the two points (so that now each of the two points is on the surface of one constructed sphere and at the center of the other). Any point that falls at the intersection of these two spheres and on the surface of the original sphere satisfies the requirement. There can be one or two such points, meaning n can be 3 or 4, but not higher. If it’s 4 then the four points are the vertices of a regular tetrahedron; if it’s 3 then the original two chosen points and one of the intersection points form an equilateral triangle (roughly, on Earth, reader Eugene Sard suggested that three such points fall at the South Pole, on Wake Island, and in southern Saudi Arabia).
| |