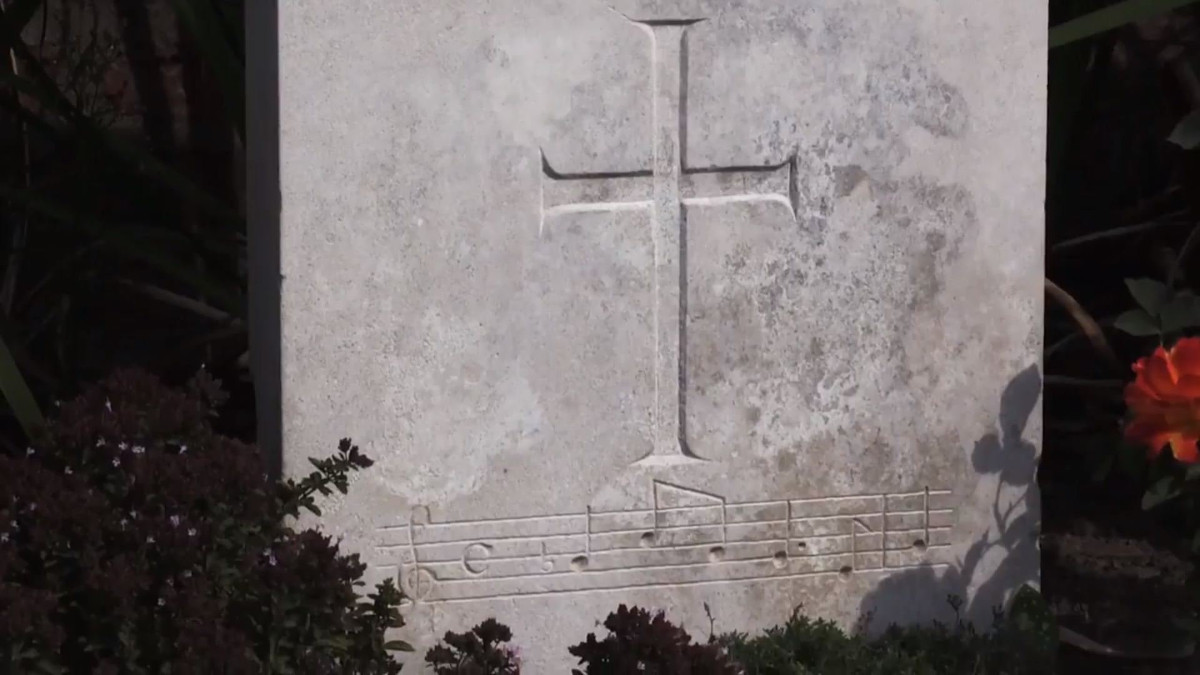Puzzles
The THOG Problem
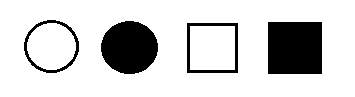
I have picked one color (black or white) and one shape (square or circle). A symbol that possesses exactly one of the properties I have picked is called a THOG. The black circle is a THOG. For each of the other symbols, is it (a) definitely a THOG, (b) undecidable, or (c) definitely not a THOG?
Cognitive psychologist Peter Wason invented this puzzle in 1979 to demonstrate some weaknesses in human thinking. In pilot studies, 0 of 10 student barristers were able to solve it correctly, with one arguing for more than an hour against the correctness of Wason’s solution. Seven of 14 medical students solved it, taking an average of 6.3 minutes. (“This is quite an impressive result.”) One young doctor solved it in his head in about a minute and said, “I would not let any doctor near me who couldn’t solve that problem.” What’s the answer?
Black and White
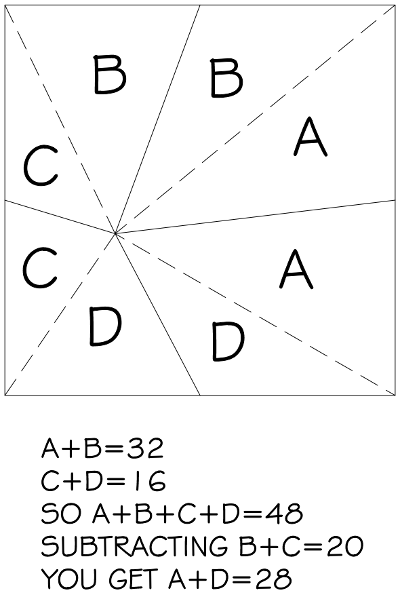
A Pretty Puzzle
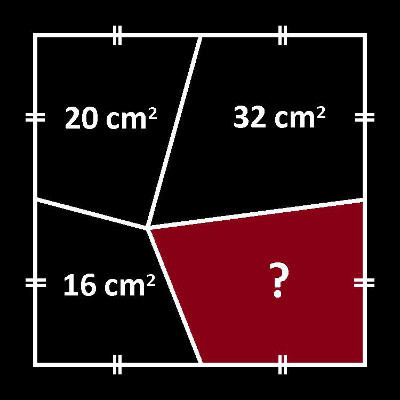
I don’t know who came up with this; I found it on r/mathpuzzles. What’s the area of the red region?
Loose Change
You’re holding a penny, and you’re standing on an infinite plane. The plane bears a grid of squares, each of which is twice the width of the penny. If you roll the penny out onto the grid, what is the probability that it will come to rest entirely within a square? (Assume the lines are of negligible thickness.)
A Memorial Puzzle
When violinist Hugh Gordon Langton was killed in World War I, the Commonwealth War Graves Commission inscribed a phrase of music (below, click to enlarge) on his headstone in Belgium’s Poelcapelle British Cemetery.
What the notes represent has been a mystery for more than a century. “They are not part of a tune that anyone has been able to discern and several have tried,” writes Sarah Wearne in Epitaphs of the Great War: Passchendaele. “In particular they are not from the song ‘After the Ball’ as some have suggested.”
Langton is the only casualty who was commemorated with a piece of music — the CWGC maintains more than a million graves and memorials worldwide, and only this one bears musical notes as an epitaph. If you can identify the tune, please contact the Commission.
A Problem From 1725
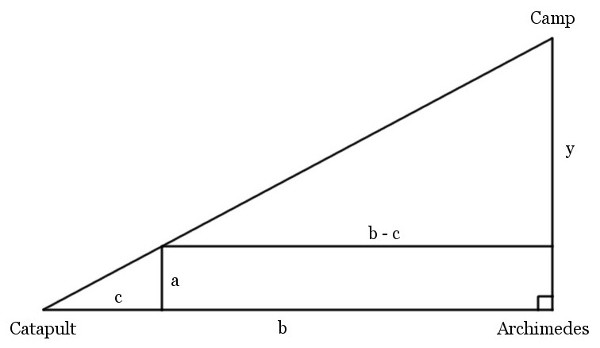
Suppose that when Marcellus besieged Syracuse, Archimedes was standing at a corner of the city wall. A ditch runs parallel to the wall, separated from it by a distance a. To Archimedes’ left at distance b along the wall stands a catapult, which is distance c from a line perpendicular to the ditch. If Archimedes’ line of sight to the camp runs perpendicular to the wall and the ditch, show that he stood a distance ab/c from the camp.
Rubik’s Clock

Hungarian sculptor and architect Ernő Rubik presented this puzzle in 1988; it was originally created by Christopher C. Wiggs and Christopher J. Taylor. The puzzle has two sides, with nine clocks on each side, and the goal is to set all the clocks to 12 o’clock simultaneously.
There are two ways to adjust the clocks. Turning a wheel at any of the four corners will adjust the clock at that corner on both sides of the puzzle. And turning a wheel will also adjust the three clocks adjacent to that corner on one side of the puzzle or the other; which side is determined by the four buttons surrounding the central clock.
So, for example, pressing the northwest button “in” and then turning the northwest wheel will adjust the northwestern quartet of clocks and the corresponding corner clock on the other side of the puzzle. Pulling the northwest button “out” and turning the same wheel will adjust the northwestern clock on the front of the puzzle, its counterpart on the back, and the three clocks adjacent to it on that side.
This is more intuitive than it sounds. Here’s a simulator.
Since there are 14 independent clocks, with 12 settings each, there are a total of 1214 = 1,283,918,464,548,864 possible configurations. It turns out that no configuration requires more than 12 moves to solve; for comparison, in the “worst case” solving a Rubik’s cube can take 20 moves. The trouble, of course, is knowing how to go about it.
Black and White
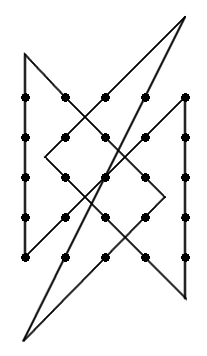
Outside the Box
An old puzzle asks: Without lifting your pencil from the paper, can you draw a series of four straight lines that passes through all nine points in this grid?

The trick is to realize that the lines can extend beyond the grid’s area:
In 1970 Solomon Golomb and John Selfridge found a way to draw a closed path of eight segments that passes through all 25 points in this grid:

Can you?