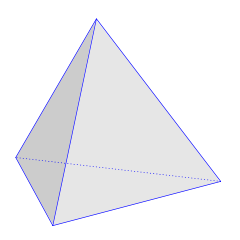
A problem from the Tenth International Mathematical Olympiad, 1968:
Prove that in every tetrahedron there is a vertex such that the three edges meeting there have lengths which are the sides of a triangle.

A problem from the Tenth International Mathematical Olympiad, 1968:
Prove that in every tetrahedron there is a vertex such that the three edges meeting there have lengths which are the sides of a triangle.
On the morning of Jan. 20, 1953, the body of 18-year-old Paul Emanuel Rubin was found at the bottom of a ditch near the Philadelphia International Airport. The coroner found there was enough cyanide in his body to “kill 10 men,” and taped to his abdomen was a 7″ x 3″ piece of paper with an enciphered message:

Rubin’s mother hadn’t seen him since the previous morning, when he’d cut some strips of adhesive tape before leaving the house. He was studying chemistry at New York University and would have had access to cyanide, but his mother said he was in good mental and physical health and hadn’t appeared worried about anything. (About 20 minutes before the body was found, the Rev. Robert M. Anderson had wished Rubin good morning; he found him “wild-eyed” and said “he was staring straight ahead and … the pupils of his eyes were dilated.”)
A friend mentioned that Rubin had been working with codes: “They’re very complicated. Anyone who reads science fiction will know what I mean.” Rubin was carrying a copy of Galaxy Science Fiction, as well as a plastic cylinder containing a signal fuse, the casing of a spent .38 caliber bullet, a “fountain pen gun” of uncertain purpose, four keys, and 47 cents. He’d had $15 when he’d left home the previous morning.
An inquest turned up nothing, and the case was closed in March. The cipher has never been solved. The Cipher Foundation has more details about the case, as well as a link to Rubin’s FBI file (8 MB PDF). The fullest account of the case that I know is in Craig Bauer’s excellent Unsolved!: The History and Mystery of the World’s Greatest Ciphers from Ancient Egypt to Online Secret Societies (2017).

This inscription was found in a cemetery of French Franciscan friars at Dole. What does it mean?
A stranger asks you to shuffle an ordinary deck of cards and then cut it into three heaps. He’ll bet you $20 that at least one of the topmost cards is a king, queen, or jack. Should you take the bet?

Here are six new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
King William’s College, on the Isle of Man, has posted the 2018 edition of its General Knowledge Paper, “The World’s Most Difficult Quiz.”
“The King William’s College General Knowledge Paper (GKP) has been frustrating and intriguing a select group of quiz connoisseurs since 1904. The paper consists of 18 sets of 10 questions, each set covering a particular theme, which in many cases is far from obvious. Cracking the theme has long been one of the attractions to devotees of the GKP.”
Answers will be published on the school website at the end of January. A warning: “A Latin phrase is always printed at the top of the quiz: Scire ubi aliquid invenire possis ea demum maxima pars eruditionis est. Freely translated, this means ‘The greatest part of knowledge is knowing where to find something’. However, be warned — using Google or a similar search engine may not always deliver the expected results!”
At the same time, the Royal Statistical Society has released its annual Christmas Quiz.
“For the last quarter-century, the Royal Statistical Society has published a fiendishly difficult Christmas quiz to entertain puzzle fans over the festive break – and this year’s special 25th anniversary edition, devised by Dr Tim Paulden, is sure to get the cogs spinning after a glass or two of mulled wine. Cracking the 15 problems below will require a potent mix of general knowledge, logic, and lateral thinking – but, as usual, no specialist mathematical knowledge is needed.” The entrant or team that scores the most points wins a subscription to the society’s magazine, Significance.
(Via MetaFilter.)
These three riddles have the same answer. What is it?
He who with his hands puts it together will not be poor, and he who buys it, does not wish to use it, and he who uses it, does not know it: now you guess what it is.
— Johannes Secundus (1511-1536)
There was a man bespake a thing
Which when the owner home did bring,
He that made it did refuse it:
And he that brought it would not use it,
And he that hath it doth not know
Whether he hath it yea or no.
— Sir John Davies (1569-1626)
There was a man who bought a thing,
The thing he bought, he did not want,
The man who sold it, could not use it,
The man who used it, did not know it.
— Every Other Saturday: A Journal of Select Reading, New and Old, April 26, 1884
A problem proposed by Charles W. Trigg in the Spring 1970 issue of the Pi Mu Epsilon Journal (Volume 5, Number 4):
The digits 1-9 can be arranged in a square array so that the digits in no column, row, or long diagonal appear in order of magnitude:
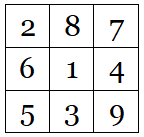
Prove that, however this is done, the central digit must be odd.