
Here are five new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.

Here are five new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.

In poker, suppose you’re dealt a pair. Is the probability that your opponent also holds a pair higher, lower, or the same as it would be if you held nothing?
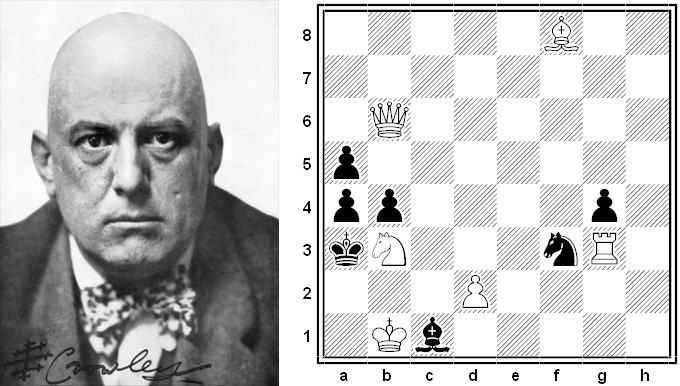
The English occultist Aleister Crowley, “the wickedest man in the world,” was a skilled chess player. In 1894 he published several problems in the Eastbourne Gazette under the pseudonym Ta Dhuibh. This one appeared on Feb. 21. How can White mate in two moves?

A problem by Kagen Schaefer:
Suppose a king tours a chessboard, visiting each square once, never crossing his own path, and finishing where he starts. Inevitably he’ll have to make some horizontal and vertical moves; for example, in the tour above he makes 14 horizontal and 16 vertical moves.
Show that in any such tour of an 8 × 8 chessboard the sum of the horizontal and vertical moves must be at least 28.
In the October 2003 issue of MIT Technology Review, Donald Aucamp offered this conundrum:
Three logicians, A, B, and C, are wearing hats. Each hat displays a positive integer, and each logician can see his companions’ numbers but not his own. All of them know that the numbers are positive integers and that one of the numbers is the sum of the other two. The three then take turns in a contest to see who can determine his number first. In the first round, all three pass, but in the second round A correctly states his number is 50. What are the other two numbers, and how did A know that his was 50?