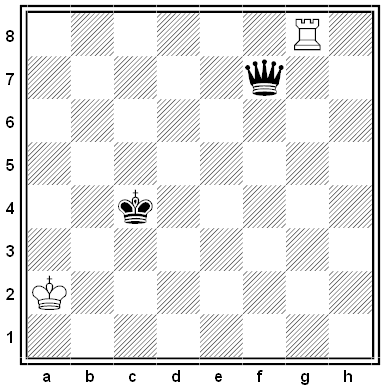
A “maximummer-selfmate” by T.R. Dawson, from 1934. White wants to force Black to checkmate him, and Black always makes the geometrically longest move available to him. How can White accomplish his goal in three moves?

A “maximummer-selfmate” by T.R. Dawson, from 1934. White wants to force Black to checkmate him, and Black always makes the geometrically longest move available to him. How can White accomplish his goal in three moves?

Another puzzle from Kendall and Thomas’ Mathematical Puzzles for the Connoisseur (1971):
Take three consecutive positive integers and cube them. Add up the digits in each of the three results, and add again until you’ve reached a single digit for each of the three numbers. For example:
463 = 97336; 9 + 7 + 3 + 3 + 6 = 28; 2 + 8 = 10; 1 + 0 = 1
473 = 103823; 1 + 0 + 3 + 8 + 2 + 3 = 17; 1 + 7 = 8
483 = 110592; 1 + 1 + 0 + 5 + 9 + 2 = 18; 1 + 8 = 9
Putting the three digits in ascending order will always give the result 189. Why?
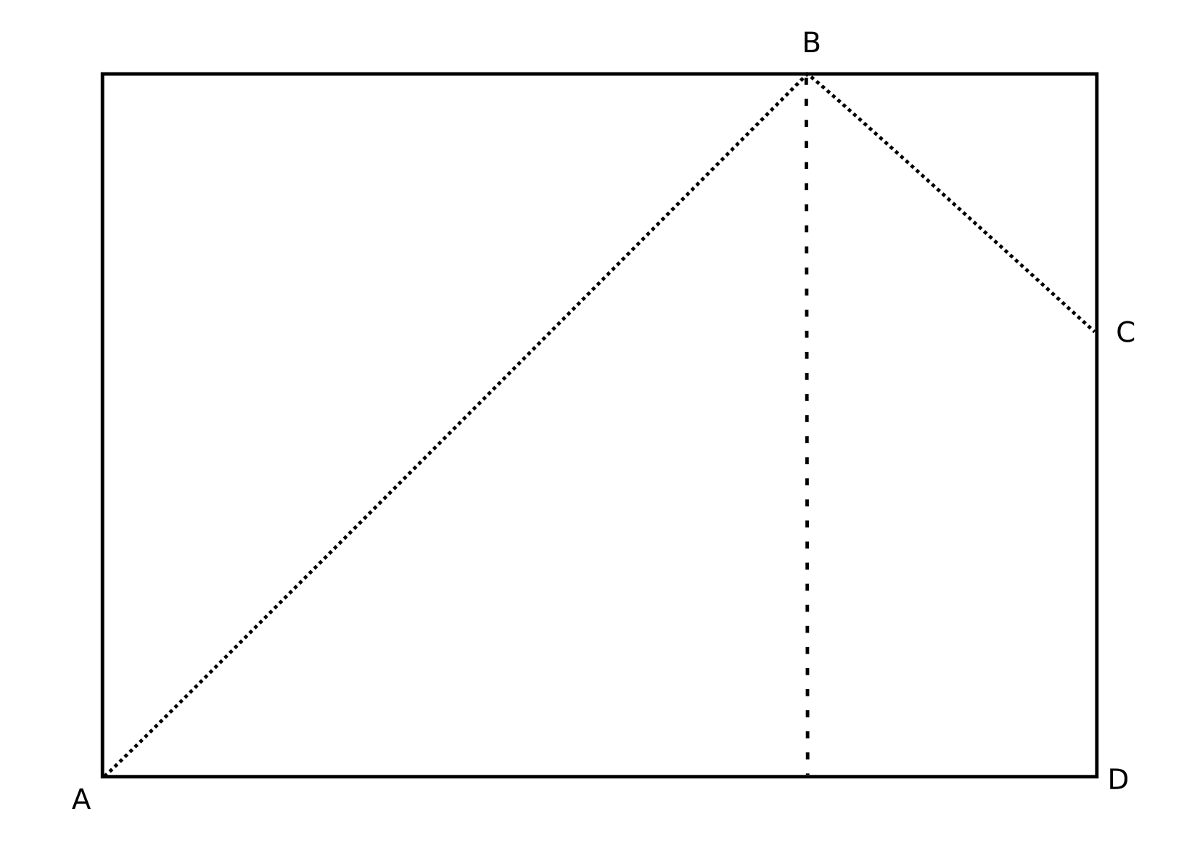
A puzzle by Matt Parker of standupmaths:
The standard paper size A4 has dimensions in the ratio . Hold a piece of A4 paper horizontally, as shown, and fold down the top left corner to meet the other side, creating fold AB, as if you were going to make a paper square. Then fold down the top right corner to meet the edge of this 1 × 1 square (making fold BC).
The perimeter of the original sheet was . What is the perimeter of the folded shape (the quadrilateral ABCD above)?
I’ll honor Matt’s request not to reveal the answer, but here’s a clue: The shape ABCD is a kite. See Matt’s video for a more visual explanation and a non-spoilery way to tell whether you have the right answer.
(Thanks to Dave Lawrence for the tip and the diagram.)
A puzzle from P.M.H. Kendall and G.M. Thomas’ Mathematical Puzzles for the Connoisseur (1962):
Start with two containers, one holding green paint and the other an equal quantity of red paint.
Assume the paints are mixed thoroughly after each operation. If the two containers are now leveled off, without pouring any paint away, so that they both contain an equal quantity of paint, which pot is now more pure, the “green” paint or the “red”?
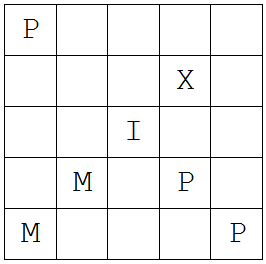
Computer science legend Donald Knuth offered this puzzle at the 29th International Puzzle Party in San Francisco in August 2009. It’s a partially completed Latin square: The challenge is to place letters in the remaining cells so that each row and column contains the same five letters and in the bottom row these spell a common English word. The solution is unique.
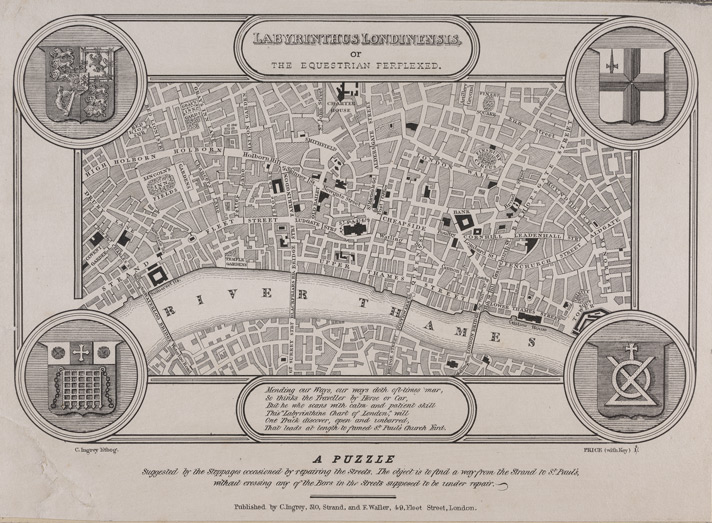
Fed up with endless traffic detours in 1830, London printer Charles Ingrey published a pointed puzzle, Labyrinthus Londoninensis, or The Equestrian Perplexed.
“The object is to find a way from the Strand [lower left] to St. Paul’s [center], without crossing any of the Bars in the Streets supposed to be under repair.”
Mending our Ways, our ways doth oft-times mar,
So thinks the Traveller by Horse or Car,
But he who scans with calm and patient skill
This ‘Labyrinthine Chart of London’, will
One Track discover, open and unbarred,
That leads at length to famed St. Pauls Church Yard.
The image above is a bit too small to navigate, but the British Library has an interactive zoomable version (requires Flash).
I don’t have the solution, but The Court Journal of Dec. 14, 1833, hints that “the farthest way round is the nearest way home.”
07/06/2022 UPDATE: A solution! (Thanks, Paul.)
A poser from Penn State mathematician Mark Levi’s Why Cats Land on Their Feet (2012):
Using only a stopwatch and a sneaker, how can you find an approximate value for ?
A puzzle from MIT Technology Review, July/August 2008:
Each of three logicians, A, B, and C, wears a hat that displays a positive integer. The number on one of the hats is the sum of the numbers on the other two. They make the following statements:
A: “I don’t know my number.”
B: “My number is 15.”
What numbers appear on hats A and C?

The president of a 100-member society receives word that the meeting place must be changed, and he needs to inform the rest of the members. He starts a telephone tree: He informs three members, each of whom informs another three members, and so on until all 100 members have received the news. Using this method, what is the greatest number of members who don’t have to make a call?