You have 10 stacks of silver dollars, with 10 coins in each stack. The coins appear identical, but you know that all the coins in one stack are counterfeit. You know the weight of a genuine coin, and you know that a counterfeit coin weighs 1 gram less than this. How many weighings must you do to find the counterfeit stack?
Puzzles
Figuring
An eight-digit number contains two 1s, two 2s, two 3s, and two 4s. The 1s are separated by 1 digit, the 2s by 2 digits, the 3s by 3 digits, and the 4s by 4 digits. What is the number?
Black and White
The Last Detail
Black and White
Late Again
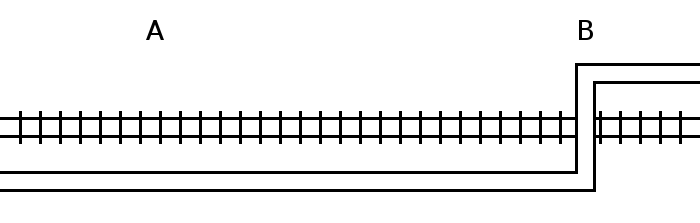
A problem from P.M.H. Kendall and G.M. Thomas’ Mathematical Puzzles for the Connoisseur, 1962: A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. What was the speed of the train?
Cheryl’s Birthday
This question appeared in the 2015 Singapore and Asian Schools Math Olympiad, a competition for 14-year-old students from Singapore, Thailand, Vietnam, China, and the U.K. (I’ve amended the language a bit):
Albert and Bernard have just become friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
| May | 15 | 16 | 19 | |||
| June | 17 | 18 | ||||
| July | 14 | 16 | ||||
| August | 14 | 15 | 17 |
Cheryl then tells Albert and Bernard separately the month and the day of her birthday, respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know it either.
Bernard: At first I didn’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
When is Cheryl’s birthday?
Singapore TV presenter Kenneth Kong posted the question online, and it went viral in a matter of days. The competition organizers had intended it to “sift out the better students” and expected that 40 percent of the competitors would find the solution. What is it?
Patrolling the Palace
A puzzle by James Tanton:
King Tricho lives in a palace in which every room is a triangle:
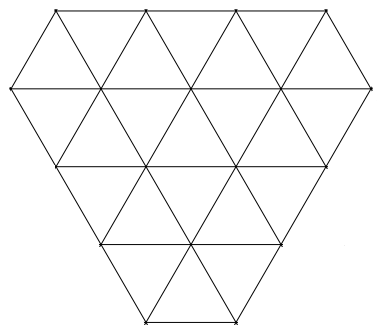
Before retiring for the night he’d like to inspect it. Is there a path that will let him visit each room once and only once? He can start anywhere.
Black and White
Spirits of the Departed

A wine merchant has three sons. When he dies, he leaves them seven barrels that are full of wine, seven that are half-full, and seven that are empty. His will requires that each son receive the same number of full, half-full, and empty barrels. Can this be done?