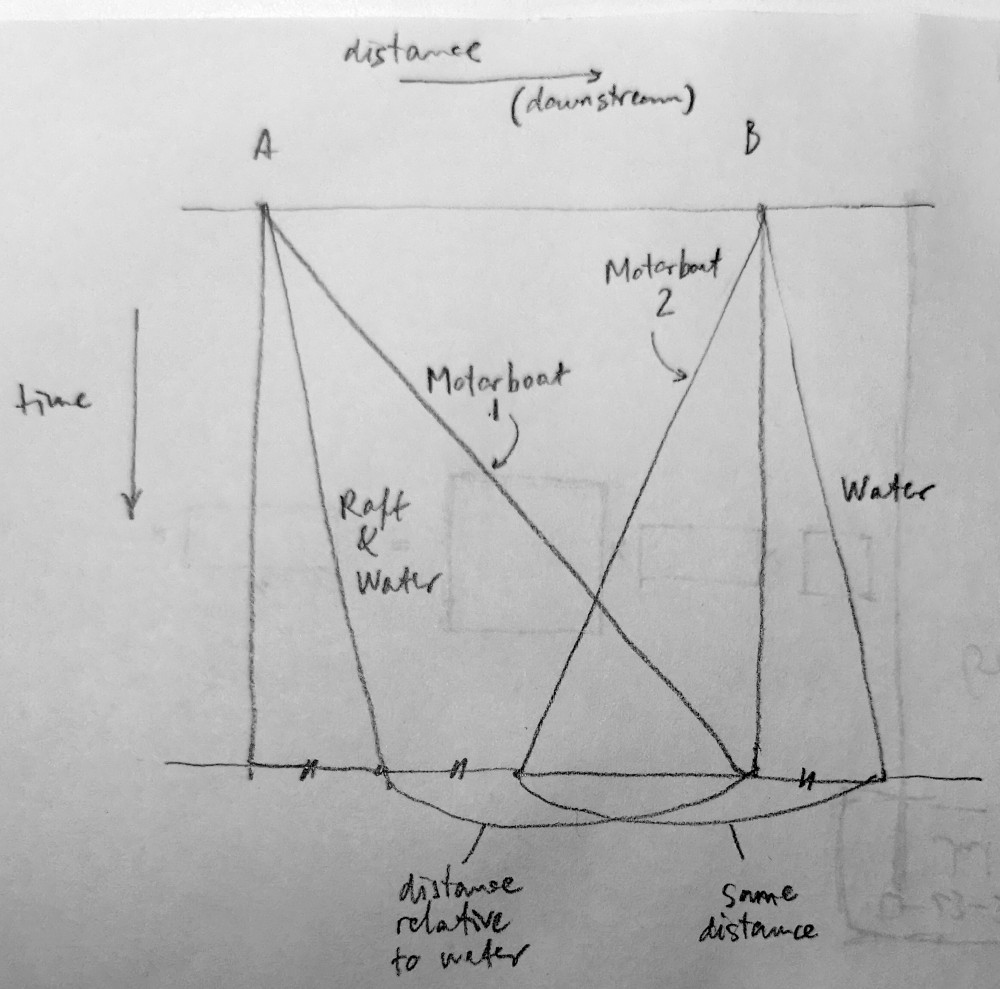
A puzzle by Ying Zhou, Daniel Irving, and Walter Gall of Rhode Island College, from the February 2012 issue of Math Horizons:
A sports team is divided into “red” and “blue” groups of 10 players each. Each player puts his belongings into a bag of his team’s color and puts it into one of 20 lockers, choosing at random. All the players leave the room. Presently one of the red team returns and can’t remember which locker is his. He and the janitor make a bet: The player can keep opening lockers so long as each bag he discovers is red. If he finds his bag, the janitor will give him $7. If not, he’ll owe the janitor $1. Should the player take the bet?