Puzzles
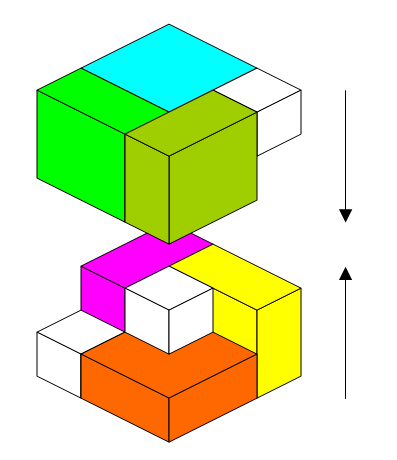
Moving Day
Is it possible to pack six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box?
Cross Purposes

A perplexing problem from the Pi Mu Epsilon Journal, Spring 1983:
In the little hamlet of Abacinia, the people use two base systems.
One resident says, “26 people use my base, base 10, and only 22 people speak base 14.”
Another says, “Of the 25 residents, 13 are bilingual and 1 is illiterate.”
All the residents speak the truth, but each (naturally) expresses numbers in her own base. How many residents are there?
Coming and Going

In 1978 the Chronicle of Higher Education mentioned an old exam question:
Q. How far can a dog run into the woods?
A. Halfway. The rest of the time he is running out.
Harvard’s Richard E. Baym wrote in to take issue with the answer:
The correct answer is ‘All the way’. Certainly we understand that the dog is running ‘in’ only until he reaches the middle of the forest, but this is in fact, all the way in. If the dog ran only half ‘in’, he would not yet be at the middle. Indeed if the dog ran halfway in and then ran halfway out, he would still be in the woods.
The editors noted, “It occurs to us that the dog’s continued presence there would be useful, in case something happens to that tree that we’ve been hearing about since high school physics — the one that falls when no one is in the forest and since there is no eardum to register sound waves, makes no noise. You know what a fine sense of hearing a dog has. Let him run halfway in (or as Mr. Baym argues, all the way), settle there, and keep an ear cocked for that tree.”
(from Robert L. Weber, ed., Science With a Smile, 1992.)
Technicalities
In presenting the rules of chess, some writers carelessly say that a pawn that reaches the eighth rank can be promoted to any piece that the player chooses. That’s a bit too generous, as a couple of puzzle composers have noted. In 1941 Leonid Kubbel presented this problem — White is to mate in two moves:

It’s not immediately clear how to release Black from his stalemate and still mate him on the next move. The solution is to promote the e7 pawn to a black king!

Now it’s Black’s move — he has to play 1. … Kd8, and White can mate both kings with 2. Qd7#!
The Polish master Johannes Zukertort offered this one: White is to mate on the move:

Here White promotes the pawn to a black knight, ending the game. (Note that it must be a knight — crazy as it seems, this is the only black piece that produces mate.)
Divide and Conquer
Facing dental surgery one day, mathematician Matt Parker asked Twitter for a math puzzle to distract him. A friend challenged him to put the digits 1-9 in order so that the first two digits formed a number that was a multiple of 2, the first three digits were a multiple of 3, and so on.
Leaving the digits in the conventional order 1234356789 doesn’t work: 12 is divisible by 2 and 123 by 3, but 1234 isn’t evenly divisible by 4. “By the end of my dental procedure, I had some but not all of the digits worked out, but, apparently, you’re not allowed to stay in the dentist’s chair after they’re finished.” At home he finished working out the solution, which is unique. What is it?
Not So Fast
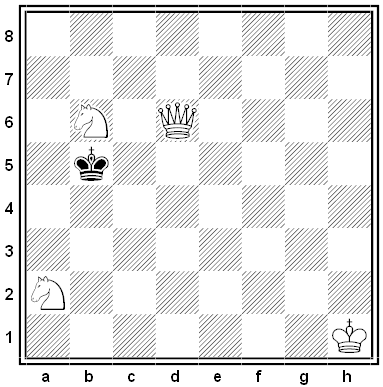
José Paluzie offered this chess poser in 1910. White is to move and mate in 1:

The key is to notice that the position is illegal: There’s no legal way for the black king to have arrived at a2. Black, desperate to avoid mate, must have put it there when White wasn’t looking.
Where did it come from? It doesn’t matter: White can place the black king on any legal square and mate in 1.
(From Burt Hochberg’s Chess Braintwisters, 1999.)
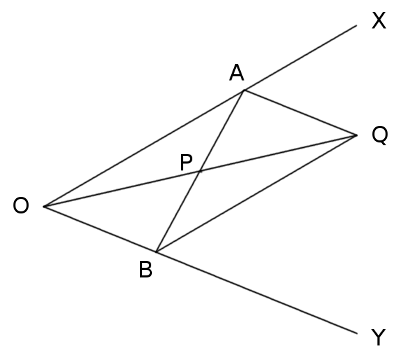
Balance
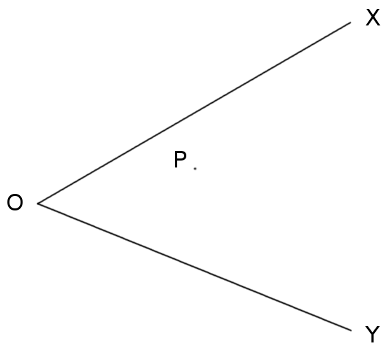
Point P lies within acute angle XOY. How can we find a point A on OX and a point B on OY such that P is the midpoint of a segment drawn between them?
A Rolling Lemon

My lousy car has an odometer without 4s — in every position, the counter advances from 3 directly to 5. For example, when it read 000039 I drove one mile and watched it roll over to 000050. Today the odometer reads 002005. How many miles has the car actually traveled?
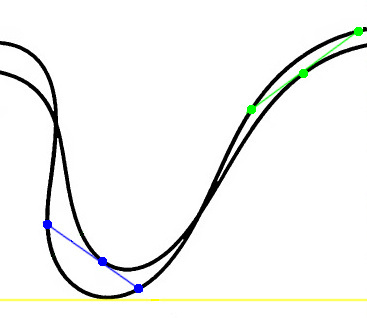
Left or Right?

You come upon the track of a bicycle in the mud. Was the bicycle traveling to the left or the right?