Puzzles
Pagan Island

Twenty-six villages are ranged around the coastline of an island. Their names, in order, are A, B, C, …, Z. At various times in its history, the island has been visited by 26 missionaries, who names are also A, B, C, …, Z. Each missionary landed first at the village that bore his name and began his work there. Each village was pagan to begin with but became converted when visited by a missionary. Whenever a missionary converted a village he would move along the coastline to the next village in the cycle A–B–C-…-Z–A. If a missionary arrived at an uncoverted village he’d convert it and continue along the cycle, but there was never more than one missionary in a village at a time. If a missionary arrived at a village that had already been converted, the villagers, feeling oppressed, would kill him and revert to a state of paganism; they would do this even to a missionary who had converted them himself and then traveled all the way around the island. There’s no restriction as to how many missionaries can be on the island at any given time. After all 26 missionaries have come and gone, how many villages remain converted?
Black and White
The Barbershop Paradox

In 1894 Lewis Carroll published a conundrum that, he wrote, presents “a very real difficulty in the Theory of Hypotheticals.” Suppose that Allen, Brown, and Carr run a shop. At least one of them must always be present to mind the shop, and whenever Allen leaves he always takes Brown with him. Now, suppose that Carr is out. In that case then if Allen is out then Brown must be in, in order to tend the shop. But we know that this isn’t true — we’ve been told that whenever Allen is out then Brown is out.
Since the supposition that Carr is out leads to a falsehood, then it must itself be false. Confusingly, the laws of logic seem to require that Carr never leave the shop.
“I greatly hope that some of the readers of Mind who take an interest in logic will assist in clearing up these curious difficulties,” Carroll wrote. Modern logicians would say that this is a simple error in reasoning, rather than a logical disaster. But what is the error?
The Falling Chain
Here are two identical rope ladders with slanting rungs. One falls to the floor, the other onto a table. The ladders are released at the same time and fall freely, but the one on the left falls faster, as if the table is “sucking” it downward. Why does this happen?
Podcast Episode 100: Lateral Thinking Puzzles

Here are five new lateral thinking puzzles to test your wits and stump your friends — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
Perspective
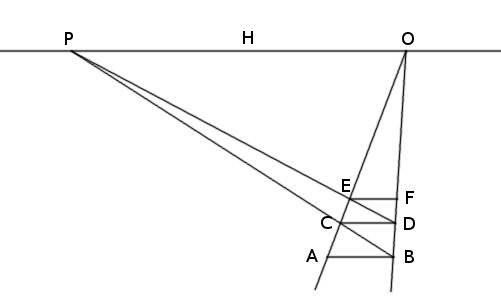
AB and CD are consecutive ties across a pair of railroad tracks that appear to meet at O on the horizon, H. If the ties are parallel to the horizon and are equally spaced along the tracks, how can we draw the next tie in this perspective figure?
Black and White
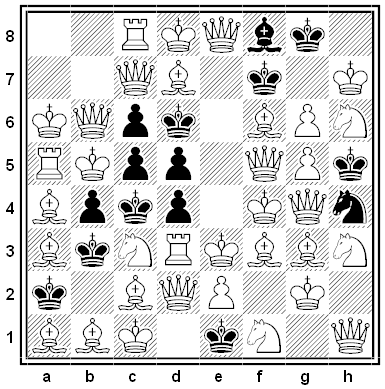
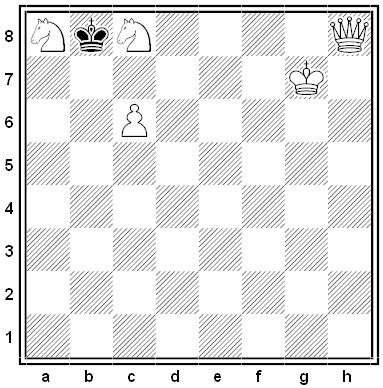
G.B. Spencer devised this ingenious diagram in 1906: It contains 16 separate chess problems, one on each rank and file. In each case, ignore the pieces not on that rank or file and find a way for White to mate in two moves.
For example, the solution to the problem on the first rank is 1. Bd4 Ke2 2. Ng3#. What are the other 15 solutions?
Reading a Pitch
In 1972, Addison-Wesley published an ad for three textbooks on the back of The American Statistician magazine. The ad began with this line:
Y LUAEB H O DTYO AOOSGL
In Word Ways, David Silverman wrote, “Care to try and figure out the hidden message? Although the slogan doesn’t have the pizzazz of (say) ‘Let Esso put a tiger in your tank’, it does have the advantage of universality; it can equally well be applied to the sale of shoes, ships or sealing wax (or, for that matter, floor wax).”
Dinner Wit
It’s said that when Frederick the Great hosted Voltaire at Sanssouci Palace, he sent him this puzzling note:
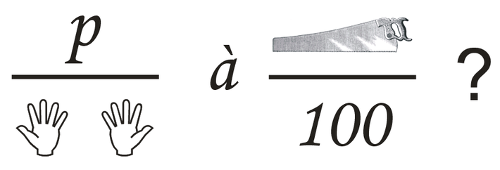
It’s a rebus in French: deux mains sous Pé à cent sous scie? (“two hands under ‘p’ at hundred under saw”) means demain souper à Sanssouci? (“supper tomorrow at Sanssouci?”).
Voltaire replied “Ga!”: Gé grand, A petit! (“big ‘G’, small ‘a’!”) means j’ai grand appétit!, or “I am very hungry!”