
White to play and mate on his first move.
(Don’t spend too much time on this — it’s a bit of a trick.)

White to play and mate on his first move.
(Don’t spend too much time on this — it’s a bit of a trick.)
In the December 2012 issue of 1 Across magazine, longtime crossword composer John Graham included a special instruction above one of his puzzles:
“I have 18dn of the 19; no 27, just 13 15; no 2 or 6 or 1dn 26 yet — plenty of 10, though I wouldn’t have chosen the timing.”
Solvers discovered that 18 down was CANCER and 19 across was OESOPHAGUS. The full message read:
“I have CANCER of the OESOPHAGUS; no CHEMOTHERAPY, just PALLIATIVE CARE; no NARCOTIC or STENT or MACMILLAN NURSE yet — plenty of MERRIMENT, though I wouldn’t have chosen the timing.”
The puzzle was reprinted as cryptic crossword No. 25,842 in the Guardian the following month.
“It seemed the natural thing to do somehow,” Graham said. “It just seemed right.” He died in November 2013, and the Guardian published a tribute crossword to remember him.
(Thanks, Anthony.)

Here’s a unique crossword puzzle by Lee Sallows. There are no clues — instead, each of the 12 entries must take the form [NUMBER](space)[LETTER](S), like so:
EIGHT BS
NINETEEN XS
ONE J
And so on. Can you complete the puzzle so that the finished grid presents an inventory of its own contents?
(A couple observations to get you started: Because the puzzle contains 12 entries, the solution will use only 12 letters. And one useful place to start is the shortest “down” entry, which is too short to be plural — it must be “ONE [LETTER]”.)

Your tedious nephews, Kerry and Kelly, are not honest, but they’re orderly. One of them lies Mondays, Tuesdays, and Wednesdays, and tells the truth on other days, and the other lies on Thursdays, Fridays, and Saturdays, and tells the truth on other days. At noon, they have the following conversation:
Kerry: I lie on Saturdays.
Kelly: I will lie tomorrow.
Kerry: I lie on Sundays.
On which day of the week does this conversation take place?

A baseball poser from Clark Kinnaird’s 1946 Encyclopedia of Puzzles and Pastimes:
“In a spring training game with the Dodgers at bat, the first man up hit a triple, the second man hit a double, the third man hit a double, the fourth man hit a single, the fifth man hit a single, the sixth man hit a single. Yet the Dodgers did not score a run in that inning. How could this have happened? These were the only men who went to bat in the inning.”
Butler University mathematician Jerry Farrell has telekinesis. Here’s a demonstration. Toss a coin and enter the result (HEAD or TAIL) as 1 Across in the grid below. Then solve the rest of the puzzle:
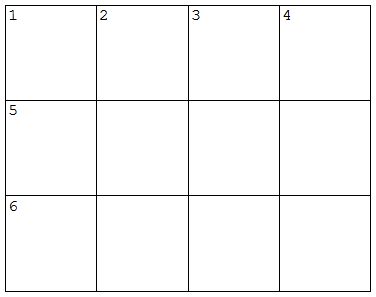
Across Down
1 Your coin shows a ______ 1 Half a laugh
5 Wagner's earth goddess 2 Station terminus?
6 Word with one or green 3 Dec follower?
4 Certain male
On the floor of a room of area 5, you place 9 rugs. Each is an arbitrary shape but has area 1. Prove that there are two rugs that overlap by at least 1/9.
In his 1943 book The Life of Johnny Reb, Emory University historian Bell Wiley collects misspellings found in the letters of Confederate soldiers. Can you decipher these words?
Bonus: What does A brim ham lillkern mean?