On the floor of a room of area 5, you place 9 rugs. Each is an arbitrary shape but has area 1. Prove that there are two rugs that overlap by at least 1/9.
Puzzles
Black and White
Puzzling Lines
In his 1943 book The Life of Johnny Reb, Emory University historian Bell Wiley collects misspellings found in the letters of Confederate soldiers. Can you decipher these words?
- agetent
- bregad
- cerce
- crawsed
- furteege
- orpital
- perperce
- porchun
- regislatury
- ridgement
Bonus: What does A brim ham lillkern mean?
A Chess Maze

By O. Wurzburg, 1919. If Black does not move at all, in how few moves can the white king reach f4? White can move only his king; as in regular play, it can capture enemy pieces but cannot enter check.
Quick Thinking
Some “ridiculous questions” from Martin Gardner:
1. A convex regular polyhedron can stand stably on any face, because its center of gravity is at the center. It’s easy to construct an irregular polyhedron that’s unstable on certain faces, so that it topples over. Is it possible to make a model of an irregular polyhedron that’s unstable on every face?
2. The center of a regular tetrahedron lies in the same plane with any two of its corner points. Is this also true of all irregular tetrahedrons?
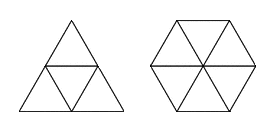
3. An equilateral triangle and a regular hexagon have perimeters of the same length. If the area of the triangle is 2 square units, what is the area of the hexagon?
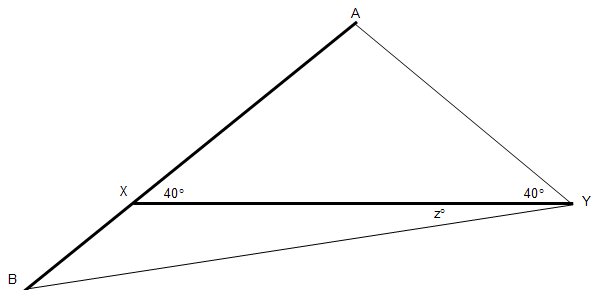
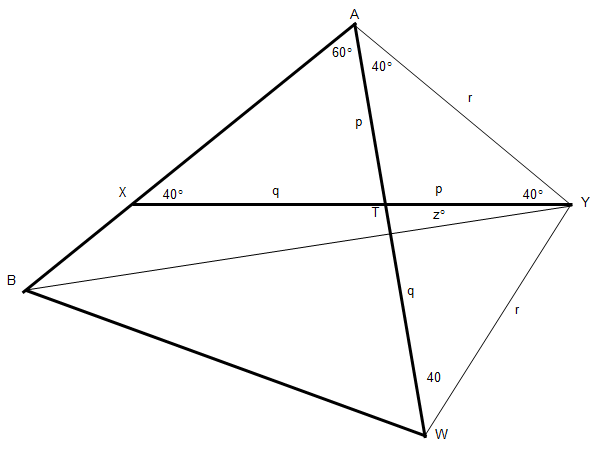
What’s the Angle?
More Fun
If the proportion of blonds among blue-eyed people is greater than among the population as a whole, is it also true that the proportion of blue-eyed people among blonds is greater than among the population as a whole?
Earnings Report

My employer has nine workers. The nine of us want to determine what our average salary is, but none of us wants to divulge his own salary. Can we find the average without doing so?
Black and White
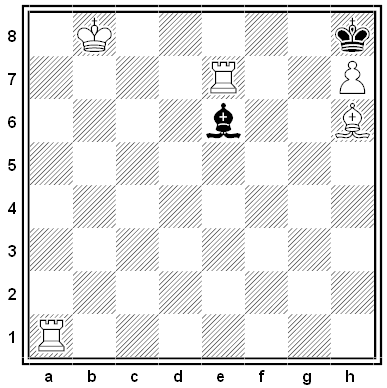
A poser by F.H. von Meyenfeldt, 1967. What move must Black play to enable a forced mate in two by White?
Remainders
Some geometric legerdemain by Argentine magician Norberto Jansenson. (Thanks, Ron.)