Puzzles
Threewise
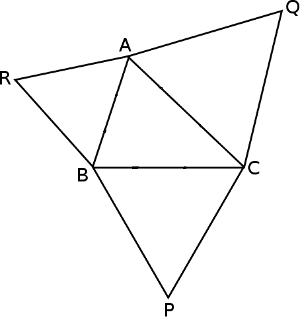
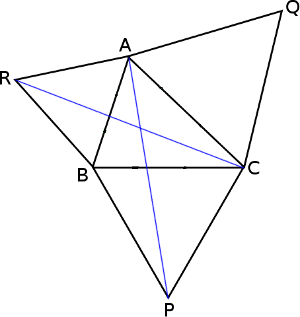
Draw an arbitrary triangle and build an equilateral triangle on each of its sides, as shown.
Now show that AP = BQ = CR.
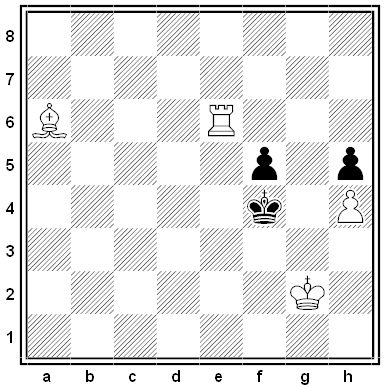
Black and White
Ice Work

Three hockey pucks, A, B, and C, lie in a plane. You make a move by hitting one puck so that it passes between the other two in a straight line. Is it possible to return all the pucks to their original positions with 1001 moves?
Knights and Scoundrels
A problem from the 1994 Italian Mathematical Olympiad:
Every inhabitant on the island of knights and scoundrels is either a knight (who always tells the truth) or a scoundrel (who always lies). A visiting journalist interviews each inhabitant exactly once and gets the following answers:
A1: On this island there is at least one scoundrel.
A2: On this island there are at least two scoundrels.
…
An-1: On this island there are at least n – 1 scoundrels.
An: On this island everyone is a scoundrel.
Can the journalist decide whether the knights outnumber the scoundrels?
“A Bit of Spanish”

This pleasing cryptarithm, by Bob High, appears in the September/October 2014 issue of MIT Technology Review. If each letter stands for a digit, what arithmetic sum is enciphered here?
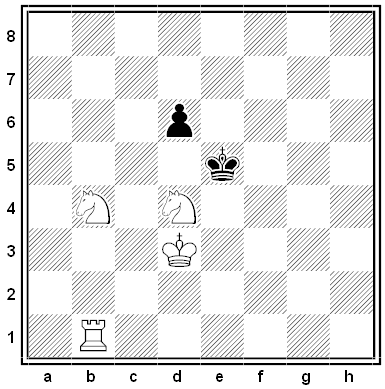
Black and White
Progress

The Martian parliament consists of a single house. Every member has three enemies at most among the other members. Show that it’s possible to divide the parliament into two houses so that every member has one enemy at most in his house.
Red and Black

Take two decks of cards, minus the jokers, shuffle them together, and divide them into two piles of 52 cards. What is the probability that the number of red cards in the Pile A equals the number of black cards in Pile B? How many cards would you have to view to be certain of your answer?