
A “simple but pretty little puzzle” by Henry Dudeney: If this flag measures 4 feet by 3 feet and presents equal areas of red and white bunting, how wide are the cross’s arms?

A “simple but pretty little puzzle” by Henry Dudeney: If this flag measures 4 feet by 3 feet and presents equal areas of red and white bunting, how wide are the cross’s arms?
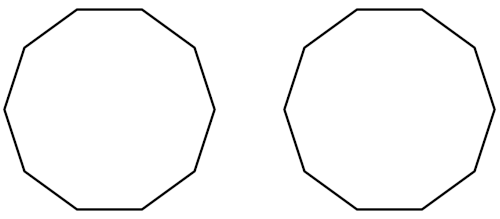
A puzzle by Russian mathematician Sergei Berlov:
Here are two decagons. Suppose that a positive integer is written at each of the 20 vertices such that the sum of the numbers around each decagon is 99. Prove that it’s possible to mark some number of successive vertices on each decagon so that the two sums of marked numbers are equal. (The marked segment on a given decagon may be a single vertex, but not all 10.)
J. Bryan III used to challenge his friends to think of an English word that contains either of the following strings of letters:
ILIL
ILIW
“I’ve never played the game with anyone who could solve either of these combinations.” Can you?
How can we make sense of this passage, composed by Willard R. Espy?
The Optic Reed has a Haste Harm. It Hose, one assumes, not to be Lever; it neither Heats the Ripple, nor Hides the Razed sinner for his Rude Rime; it is not Old. Then Leave to it; ere thy grave Loses, thou mayst find here the Hart to the Rest thou Ravest to Limb.
A circle is divided into six sectors, into which are written (say, counterclockwise) these numbers:
1, 0, 1, 0, 0, 0
You can increase any two neighboring numbers by 1. By doing this repeatedly, is there a way to make all six numbers equal?
A problem by Nikolai Rozov:
“If the brainteaser you solved before you solved this one was harder than the brainteaser you solved after you solved the brainteaser that you solved before you solved this one, was the brainteaser you solved before you solved this one harder than this one?”

By Wikimedia user Efbrazil. Fill in four squares to make a continuous dark path connecting the stars. No diagonal moves are allowed.
Back in 2017 I wrote about the Feynman ciphers, three coded messages that had been presented as challenges to Richard Feynman in the 1950s.
Feynman couldn’t crack them, and even at the time of my post only the first of the three had been decoded — it turned out to be a transposition of the opening of Chaucer’s Canterbury Tales in Middle English. But in May 2023 David Vierra solved the other two — one turns out to be an excerpt from A.E. Housman’s 1896 poem “Terence, This is Stupid Stuff,” and the other is the start of Feynman’s 1953 paper “Atomic Theory of the λ Transition in Helium,” from The Physical Review.
Who was the “fellow scientist” who had devised these challenges? Nick Pelling thinks the most likely candidate is Paul Olum, who had been Feynman’s officemate at Los Alamos in the 1940s, but hard evidence is lacking. More at Cipher Mysteries.
(Thanks to reader Peter Dawyndt for the tip.)
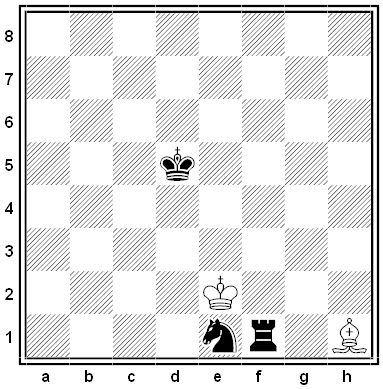
Smith College mathematician Jim Henle published this retrograde analysis puzzle in the Mathematical Intelligencer in 2018 as part of an appreciation of Raymond Smullyan. “After many moves, the chessboard appears as above. What were the last two moves?”
A Polish problem longlisted for the 19th International Mathematical Olympiad in Yugoslavia, July 1977:
A room contains nine men. Among every three of them there are two who are mutually acquainted. Prove that four of them are mutually acquainted.