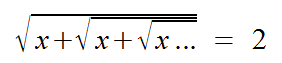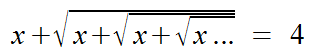Puzzles
Dog’s Mead

This puzzle was devised by W.T. Williams. The goal is to discover the age of Father Dunk’s mother-in-law (2 down), but the clues contain so much cross-reference and the grid so many interlocking solutions that practically the whole puzzle must be completed to find it.
The year is 1939. There are 20 shillings in a pound; 4840 square yards in an acre; a quarter of an acre in a rood; and 1760 yards in a mile.
ACROSS
1. Area in square yards of Dog’s Mead
5. Age of Martha, Father Dunk’s aunt
6. Difference in yards between length and breadth of Dog’s Mead
7. Number of roods in Dog’s Mead times 8 down
8. The year the Dunks acquired Dog’s Mead
10. Father Dunk’s age
11. Year of Mary’s birth
14. Perimeter in yards of Dog’s Mead
15. Cube of Father Dunk’s walking speed in miles per hour
16. 15 across minus 9 down
DOWN
1. Value in shillings per rood of Dog’s Mead
2. Square of the age of father Dunk’s mother-in-law
3. Age of Mary, father Dunk’s other daughter
4. Value in pounds of Dog’s Mead
6. Age of Ted, father Dunk’s son, who will be twice the age of his sister Mary in 1945
7. Square of the breadth of Dog’s Mead
8. Time in minutes it takes Father Dunk to walk 4/3 times round Dog’s Mead
9. The number which, when multiplied by 10 across, gives 10 down
10. See 9 down
12. Addition of the digits of 10 down plus 1
13. Number of years Dog’s Mead has been in the Dunk family
Hint: Start with 15 across, and keep your wits about you — most of the clues require some sort of insight or intelligent narrowing of the possible solutions; there’s very little mechanical plugging of numbers. With enough careful, dogged reasoning, it’s possible to complete the entire grid, but it’s stupendously hard.
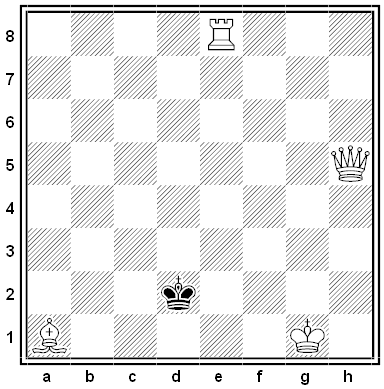
Black and White
Emptied Nest
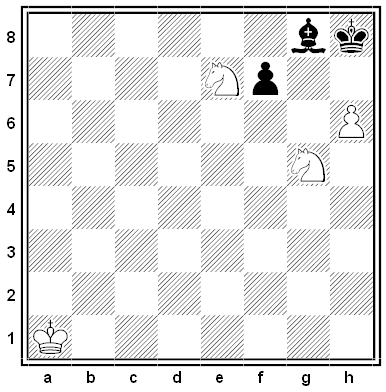
Black and White
Short-Handed
Suppose we have a clock whose hour and minute hands are identical. How times times per day will we find it impossible to tell the time, provided we always know whether it’s a.m. or p.m.?
Ice Water
A boat floats in a swimming pool. In the boat is a block of ice. If the block is dumped into the water and melts, does the water level rise or fall?
The Broken Deck
When eight certain cards are removed from a standard poker deck, it becomes impossible to deal a straight flush. What are the cards? (Assume the deck contains no jokers.)
Black and White
Bootstrap Percolation

On a 12 × 12 grid, some squares are infected and some are healthy. On each turn, a healthy square becomes infected if it has two or more infected orthogonal neighbors. (In the example above, the black squares are infected, the white squares are healthy, and the gray squares will be infected next turn.) What’s the smallest number of initially infected squares that can spread an infection over the whole board?