Puzzles
Alcohol Problem

A bottle of fine wine normally improves with age for a while, but then goes bad. Consider, however, a bottle of EverBetter Wine, which continues to get better forever. When should we drink it?
— John L. Pollock, “How Do You Maximize Expectation Value?”, Noûs, September 1983
See The Devil’s Game.
Out of Sight
Several spherical planets of equal size are floating in space. The surface of each planet includes a region that is invisible from the other planets. Prove that the sum of these regions is equal to the surface area of one planet.
Bad Behavior
You and I drive from Los Angeles to Las Vegas in separate cars. We depart simultaneously, and you stay always ahead of me, dutifully driving the speed limit throughout the trip. Nonetheless I get ticketed for speeding. How?
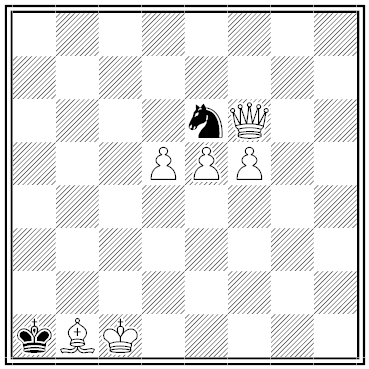
Black and White
Animal Behavior
Martian snakes are elastic. If you take the tail of a Martian snake, and I take the head, and we pull in opposite directions, will there always be a part of the snake that doesn’t move?
Reverses
A Hungarian problem shortlisted for the 30th International Mathematical Olympiad, 1989:
Around a circular race track are n race cars, each at a different location. At a signal, each car chooses a direction and begins to drive at a constant speed that will take it around the course in 1 hour. When two cars meet, both reverse direction without loss of speed. Show that at some future moment all the cars will be at their original positions.
Black and White
Weather Report
A puzzle contributed by Howard C. Saar to Recreational Mathematics Magazine, October 1962:
On the day before yesterday, the weatherman said, “Today’s weather is different from yesterday’s. If the weather is the same tomorrow as it was yesterday, the day after tomorrow will have the same weather as the day before yesterday. But if the weather is the same tomorrow as it is today, the day after tomorrow will have the same weather as yesterday.”
It is raining today, and it rained on the day before yesterday. What was the weather like yesterday? (Note: The prediction was correct!)
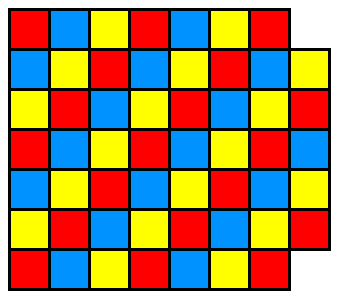
Coverup

Two squares have been removed from this 8×7 rectangle. Can the remaining 54 squares be tiled orthogonally with 18 3×1 tiles?