The digits 123456789 can be arranged to form 362,880 distinct 9-digit numbers.
How many of these are prime?
The digits 123456789 can be arranged to form 362,880 distinct 9-digit numbers.
How many of these are prime?

Alan and Bob are playing a game of marbles. Alan has two marbles, Bob has one, and each rolls to try to come nearest to a fixed point. If the two have equal skill, what is the chance that Alan will win?
There seem to be two contradictory arguments. On the one hand, each of the three marbles has an equal chance of winning, and two of them belong to Alan, so it seems that there’s a 2/3 chance that Alan will win.
On the other hand, there are four possible outcomes: (a) both of Alan’s rolls are better than Bob’s, (b) Alan’s first roll is better than Bob’s, but his second is worse, (c) Alan’s first roll is worse than Bob’s, but his second is better, and (d) both of Alan’s rolls are worse than Bob’s. In 3 of the 4 cases, Alan wins, so it appears that his overall chance of winning is 3/4.
Which argument is correct?
A riddle attributed to British prime minister George Canning, among many others:
A word there is of plural number,
Foe to ease and tranquil slumber.
Any other word you take
And add an S will plural make;
But if you add an S to this,
So strange the metamorphosis,
Plural is plural now no more
And sweet what bitter was before.
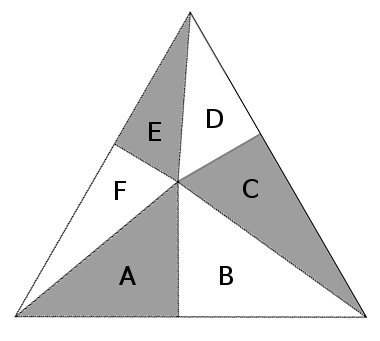
Choose an arbitrary point inside an equilateral triangle and draw segments to the vertices and perpendiculars to the sides. This divides the triangle into six smaller triangles, A, B, C, D, E, and F. Prove that the areas A + C + E and B + D + F are equal.
A 10×10 chessboard contains 41 rooks. Prove that there are five rooks that don’t attack one another.
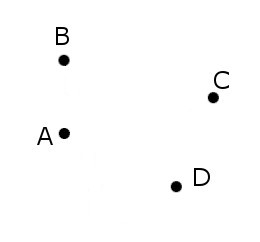
A “coffin,” or killer problem, from the oral entrance exams to the math department of Moscow State University:
Construct (with ruler and compass) a square given one point from each side.