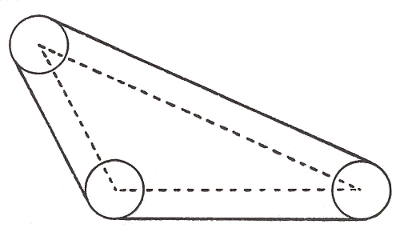
A puzzle by Harry Langman:
A thin belt is stretched around three pulleys, each of which is 2 feet in diameter. The distances between the centers of the pulleys are 6 feet, 9 feet, and 13 feet. How long is the belt?

A puzzle by Harry Langman:
A thin belt is stretched around three pulleys, each of which is 2 feet in diameter. The distances between the centers of the pulleys are 6 feet, 9 feet, and 13 feet. How long is the belt?
Helen Fouché Gaines’ 1956 textbook Cryptanalysis: A Study of Ciphers and Their Solution concludes with a cipher that, she says, “nobody has ever been able to decrypt”:
VQBUP PVSPG GFPNU EDOKD XHEWT IYCLK XRZAP VUFSA WEMUX GPNIV QJMNJ JNIZY KBPNF RRHTB WWNUQ JAJGJ FHADQ LQMFL XRGGW UGWVZ GKFBC MPXKE KQCQQ LBODO QJVEL.
It was still unsolved in 1968, when Dmitri Borgmann, editor of the Journal of Recreational Linguistics, urged his readers to tackle the problem: “Are you going to let this challenge lie there, taunting you for the rest of your lives? Or are you going to get busy and solve that pesky little crypt?”
As far as I can tell, they let it lie there, and it remains unsolved to this day. Any ideas? There are few clues in Gaines’ book. The cipher is the last in a series of exercises at the end of a chapter titled “Investigating the Unknown Cipher,” and she gives no hint as to its source. Of the exercises, she writes, “there is none in which the system may not be learned through analysis, unless perhaps the final unnumbered cryptogram.” The solution says simply “Unsolved.”
From a 1921 essay by A.A. Milne:
TERALBAY is not a word which one uses much in ordinary life. Rearrange the letters, however, and it becomes such a word. A friend — no, I can call him a friend no longer — a person gave me this collection of letters as I was going to bed and challenged me to make a proper word of it. He added that Lord Melbourne — this, he alleged, is a well-known historical fact — Lord Melbourne had given this word to Queen Victoria once, and it had kept her awake the whole night. After this, one could not be so disloyal as to solve it at once. For two hours or so, therefore, I merely toyed with it. Whenever I seemed to be getting warm I hurriedly thought of something else. This quixotic loyalty has been the undoing of me; my chances of a solution have slipped by, and I am beginning to fear that they will never return. While this is the case, the only word I can write about is TERALBAY.
The answer is not RATEABLY, or BAT-EARLY, which “ought to mean something, but it doesn’t.” Rudolf Flesch notes that TRAYABLE is not a word, and that, though TEARABLY appears in small type in Webster’s Unabridged, “it obviously won’t do.”
What’s the answer? There’s no trick — it’s an ordinary English word.
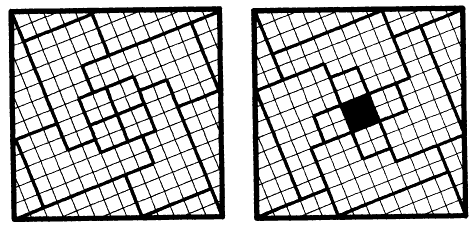
Martin Gardner called this the proudest puzzle of his own devising. When the pieces on the left are rearranged as on the right, a hole appears in the center of the square. How is this possible?
“I haven’t the foggiest notion of how to succeed in inventing a good puzzle,” he told the College Mathematics Journal. “I don’t think psychologists understand much either about how mathematical discoveries are made. … The creative act is still a mystery.”