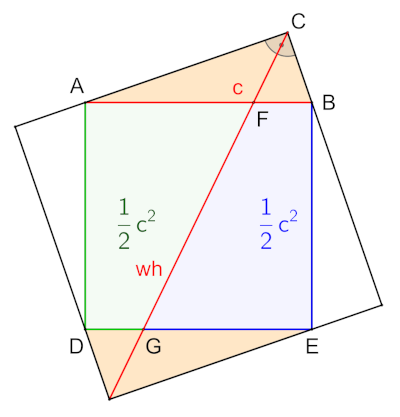
In any right triangle, the angle bisector of the right angle divides the square on the hypotenuse into two congruent trapezoids.

In any right triangle, the angle bisector of the right angle divides the square on the hypotenuse into two congruent trapezoids.
fIVe + sIX + seVen
5 + 6 + 7 = 18
IV + IX + V = 18
These are the only three consecutive numbers whose sum equals that of the Roman numerals embedded in their names.

The sea urchin Coelopleurus exquisitus was discovered on eBay. Marine biologist Simon Coppard was directed to a listing on the site in 2004 and realized that the species had not previously been described. When it was properly named and introduced in Zootaxa two years later, the value of specimens on eBay shot up from $8 to $138.
In 2008 a fossilized aphid on eBay was similarly found to be unidentified. Eventually it was named Mindarus harringtoni, after the buyer.
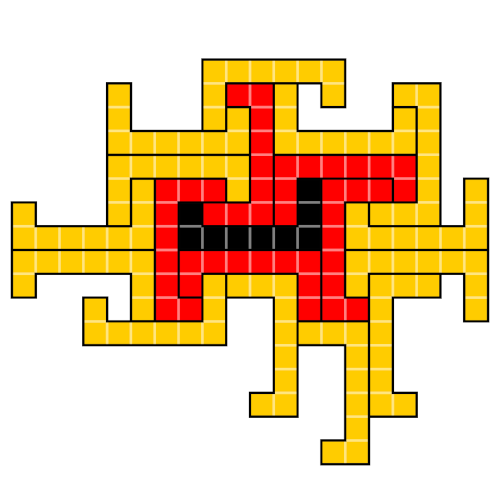
The dark polyomino at the center of this figure, devised by Craig S. Kaplan, has an unusual property: It can be surrounded snugly with copies of itself, leaving no overlaps or gaps. In this case, the “corona” (red) can be surrounded with a second corona (amber), itself also composed of copies of the initial shape. But that’s as far as we can get — there’s no way to create a third corona using the same shape.
That gives the initial shape a “Heesch number” of 2 — the designation is named for German geometer Heinrich Heesch, who had proposed this line of study in 1968.
Shapes needn’t be polyominos: Heesch himself devised the example below, the union of a square, an equilateral triangle, and a 30-60-90 triangle:
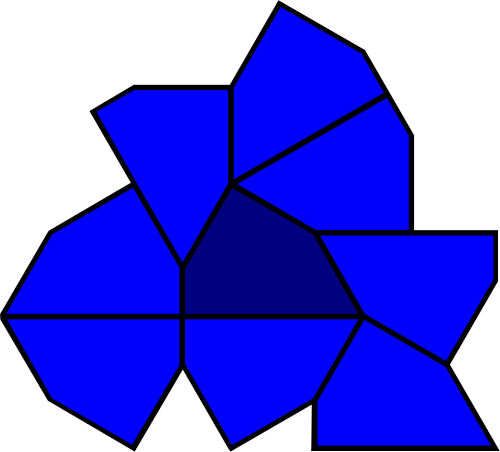
It earns a Heesch number of 1, as it can bear only the single corona shown.
Can all positive integers be Heesch numbers? That’s unknown. The Heesch number of the square is infinite, and that of the circle is zero. The highest finite number reached so far is 6.
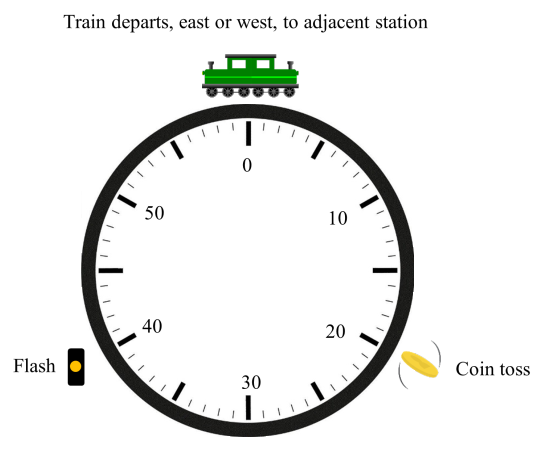
A train line extends infinitely far east and west. Stations are spaced a mile apart, and midway between each pair of stations is a signal light. There’s one train on the line, and it moves to an adjacent station at the top of each hour. Its choice (east or west) is determined by the engineer, who flips a coin 20 minutes after each hour. If the coin lands heads, the train’s next destination will be the station one mile east. If it lands tails, the train will next go to the station one mile west.
Forty minutes after each hour, one of the infinitely many signal lights will flash. The flash is visible all along the line. The identity of the flashing light is random, and it’s unrelated to the coin toss.
You wake up on this train while it’s stopped at a station. It’s 2:30 p.m., which means the engineer flipped his coin 10 minutes ago. The conductor tells you that the next destination is Willoughby. A map tells you that the Willoughby station is flanked by East Willoughby and West Willoughby, so you must be at one of these two stations, but you don’t know which one. Because these are the only two possibilities and there’s no reason for one to be more likely, you conclude that they’re equally probable.
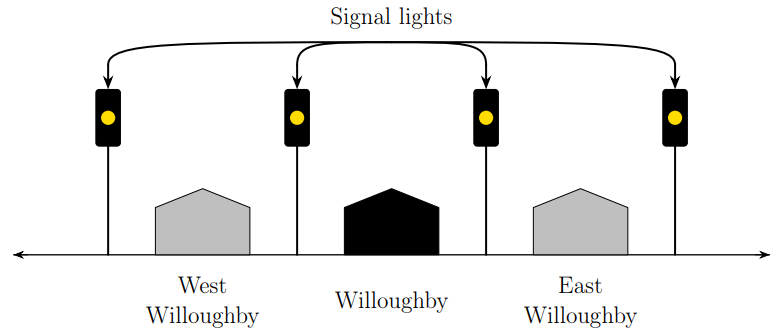
Before the train departs at 3 p.m., is it possible to guess the outcome of the engineer’s coin toss at 2:20 p.m. with success probability greater than 1/2? El Camino College mathematician Leonard M. Wapner contends that it is. At 2:40 p.m. a signal light will flash. There’s a nonzero probability p that the light that flashes will be one of the two lights adjacent to the Willoughby station. If that happens, it will indicate with certainty the direction of Willoughby (east or west) from your current location. The chance that the flash doesn’t come from one of these two lights is 1 – p, and in that case the chance is 1/2 that it comes from the direction of Willoughby. Overall:
“So,” Wapner writes, “if the light flashes to your east, you would guess that the train will be departing to the east and that the engineer’s coin landed heads. If the light flashes to the west, you would guess that the train will depart to the west and that the engineer’s coin landed tails. You should expect your guess (east/heads or tails/west) to be successful more often than not.”
(He adds, “The Willoughby prediction scheme, though mathematically valid, is far too contrived for it to be achieved in actuality. But there being no mathematical contradictions, the door remains open to variations and applications.”)
(Leonard M. Wapner, “Beyond Chance: Predicting the Unpredictable,” Recreational Mathematics Magazine 12:21 [December 2025], 1-8.)
In 1943 Buckminster Fuller announced that he’d been getting by on two hours of sleep a day. Each person has a primary and a secondary store of energy, he said; the first is restored quickly and the second takes longer. The trick, then, is to relax as soon as you’ve used up the primary store. Fuller trained himself to take a nap at the first sign of fatigue, which he found happened about every six hours. Taking a half-hour nap at those times left him in “the most vigorous and alert condition I have ever enjoyed,” he said.
“For two years Fuller thus averaged two hours of sleep in 24,” Time reported, adding, “Life-insurance doctors who examined him found him sound as a nut.” Fuller said he’d had to abandon the plan because it conflicted with his coworkers’ schedules. “But he wishes the nation’s ‘key thinkers’ could adopt his schedule; he is convinced it would shorten the war.”
Take a whole number, reverse the order of its digits, and subtract one from the other. The difference will always be evenly divisible by 9.
Does this remain true if we just scramble the digits of the first number, rather than reversing them?
A performer takes 21 cards from a standard deck and shuffles them. A player notes one at random. The performer deals out the cards into three columns of seven cards each. The player indicates the column that contains her card. Twice more the performer deals out the cards into three columns and the player identifies the one containing her card. At this point the performer identifies the card.
How is this done? The trick works automatically so long as, in taking up the cards, the performer always puts the chosen pile between the other two. After the first deal, the chosen card will fall in one of positions 8-14; after the second deal, it will reach position 10-12; and after the last deal, it will be the 11th card in the assembled packet (at which point the performer can reveal it however he pleases).
This illustration, by CMG Lee, demonstrates the same principle using 27 cards. At each step, the pile containing the chosen card is shaded yellow; the numbers correspond to the step numbers. In this case the chosen card always finds its way to the 14th position.
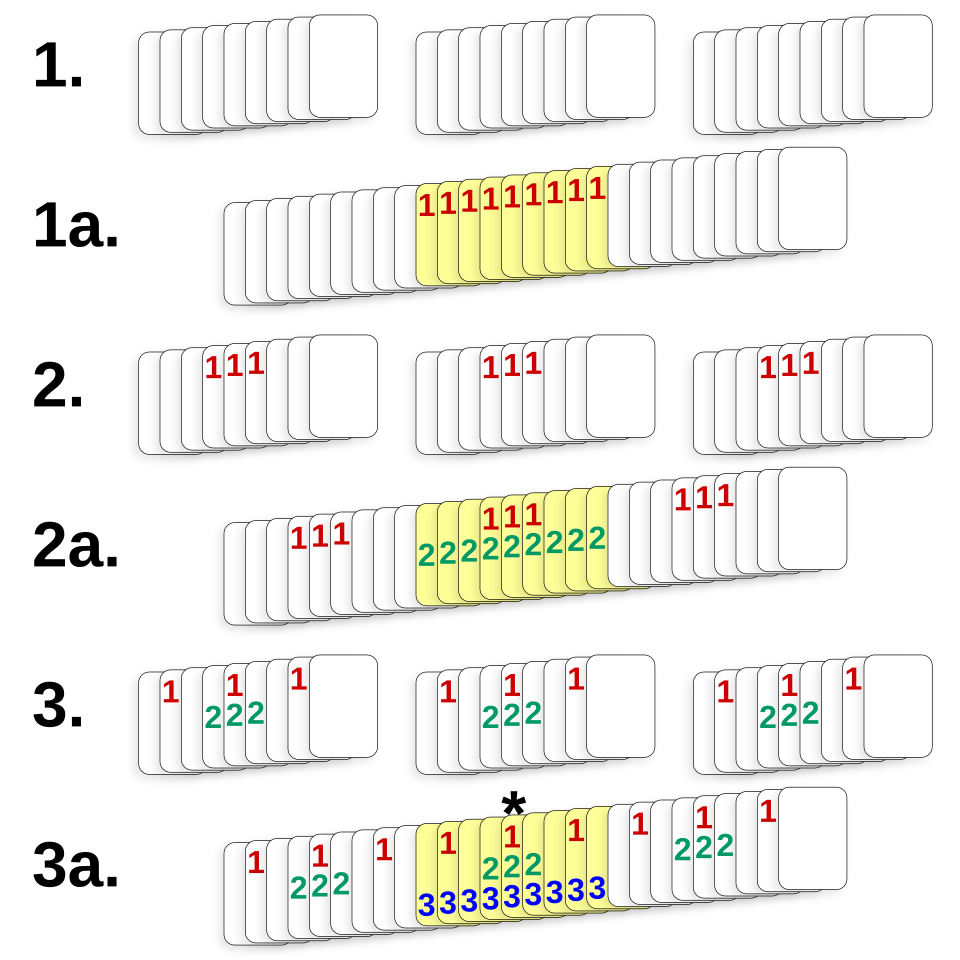
Here’s an animation with 21 cards, in which the chosen card, marked with an X, finds its way to the 11th position:

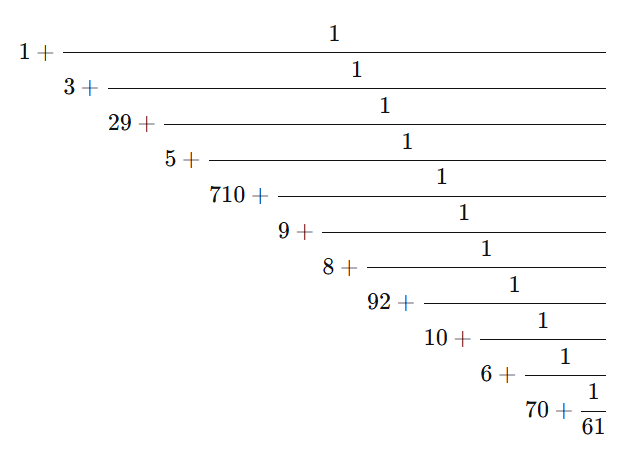
From reader Giorgos Kalogeropoulos:
“This continued fraction converges to a constant and this constant is the terms of the continued fraction concatenated.”
Constant: 1.329571098921067061816694798131449807696979288539287861665690554139889293716015345375844973593801890…
Terms: 1, 3, 29, 5, 710, 9, 8, 92, 10, 6, 70, 61, 81, 66, 94, 7, 98, 13, 14, 4, 980, 76, 96, 97, 928, 85, 39, 2, 87, 86, 16, 65, 690, 55, 41, 398, 89, 293, 71, 60, 15, 34, 53, 75, 84, 49, 73, 59, 380, 18, 90…
“This is the lexicographically earliest sequence starting with {1,3…}.”
(Thanks, Giorgos.)