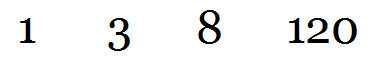Cartoon laws of physics:
- Any body suspended in space will remain in space until made aware of its situation. Daffy Duck steps off a cliff, expecting further pastureland. He loiters in midair, soliloquizing flippantly, until he chances to look down. At this point, the familiar principle of 32 feet per second per second takes over.
- Any body in motion will tend to remain in motion until solid matter intervenes suddenly. Whether shot from a cannon or in hot pursuit on foot, cartoon characters are so absolute in their momentum that only a telephone pole or an outsize boulder retards their forward motion absolutely. Sir Isaac Newton called this sudden termination of motion the stooge’s surcease.
- Any body passing through solid matter will leave a perforation conforming to its perimeter. Also called the silhouette of passage, this phenomenon is the specialty of victims of directed-pressure explosions and of reckless cowards who are so eager to escape that they exit directly through the wall of a house, leaving a cookie-cutout-perfect hole. The threat of skunks or matrimony often catalyzes this reaction.
- The time required for an object to fall twenty stories is greater than or equal to the time it takes for whoever knocked it off the ledge to spiral down twenty flights to attempt to capture it unbroken. Such an object is inevitably priceless, the attempt to capture it inevitably unsuccessful.
There are 10 laws altogether, including “9. Everything falls faster than an anvil.” As early as 1956 Walt Disney was describing the “plausible impossible.” In Who Framed Roger Rabbit, Eddie Valiant says, “Do you mean to tell me you could’ve taken your hand out of that cuff at any time?” Roger answers, “Not at any time! Only when it was funny!”