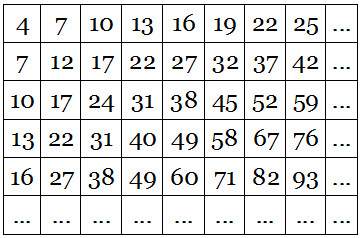
Another interesting item from James Tanton’s Mathematics Galore! (2012):
Write down a sequence of positive integers that never decreases. The list can include duplicates. As an example, here’s a list of primes:
2, 3, 5, 7, 11, 13
Call the sequence pn. Now, a “frequency sequence” records the number of members less than 1, less than 2, and so on. For the list of primes above, the frequency sequence is:
0, 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6
Pleasingly, the frequency sequence of the frequency sequence of pn is pn. That is, if we take the frequency sequence of the list 0, 0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6 above, we get 2, 3, 5, 7, 11, 13 again.
Now add position numbers to each of the two lists, pn and its frequency sequence — that is, add 1 to the first element of each, 2 to the second, and so on. With the primes that gives us:
Pn: 3, 5, 8, 11, 16, 19 …
Qn: 1, 2, 4, 6, 7, 9, 10, 12, 13, 14, 15, 17, 18, 20 …
These two sequences will always be complementary — all the counting numbers appear, but they’re split between the two sequences, with no duplicates.