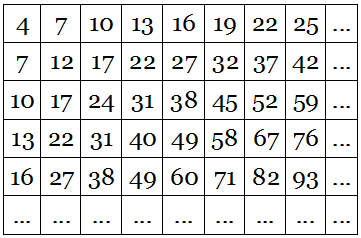
Biologist F.W. Went points out that the physical size of human beings was a critical factor in their mastery of fire. Any flame must maintain a certain size in order to sustain the ignition temperature of its fuel, and a wood or coal fire in particular radiates so much heat that it must maintain a fairly large critical mass in order to keep burning; a small fire will go out.
“Interestingly enough,” Went writes, “a wood or coal fire above the critical size produces just the right amount of heat to warm man in a cave, or a room, or a camping site. But ants or small rodents would have to keep too far away to make a fire economical, or rather, they would be unable to bring up enough wood to keep the fire going. Therefore in an ant society fire is not an economical possibility, and they have developed without its benefits, by operating only while outside temperatures are within the physiological range. Man on the other hand has been able to move into very cold areas by using fire.”
“Man, with his remarkable brain, developed the use of fire, but … only a creature of man’s size could effectively control that fire,” writes Peter S. Stevens in Patterns in Nature (1974). “It happens that a small campfire is the smallest fire that is reliable and controllable. A still smaller flame is too easily snuffed out and a larger one too easily gets out of control. Prometheus was just large enough to feed the flames and to keep from getting burnt.”
(F.W. Went, “The Size of Man,” American Scientist, 56:4 [Winter 1968], 400-413.)