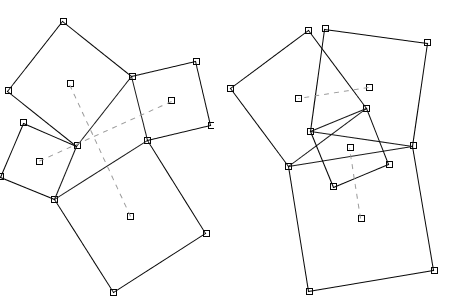
Draw any quadrilateral and build a square on each of its sides.
Connect the centers of opposite squares, and these two line segments will be perpendicular and of equal length.

Draw any quadrilateral and build a square on each of its sides.
Connect the centers of opposite squares, and these two line segments will be perpendicular and of equal length.
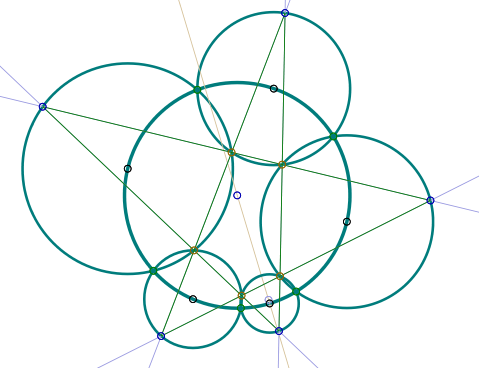
If the centers of five circles lie along the circumference of a sixth so that they overlap like the links of a chain, and if each intersects its neighbor on the sixth circle as well, then drawing lines as shown through the remaining intersections will form a pentagram whose points lie on the five circles.
A 19th-century schoolchild defined a circle as “a round straight line with a hole in the middle.”

Entomologist Alexandre Girault expressed himself in his work. Of the 500 genera he named, many honored artists, poets, and writers whom he admired: Davincia, Shakespearia, Beethovena, Mozartella, Emersonia, Raphaelana, Ovidia, Goetheana, Thoreauella, Tennysoniana, Bachiana, Keatsia, Plutarchia, Schilleria, Aeschylia, Aligheria, Thalesanna, Rubensteina, Carlyleia, Herodotia, Cowperella, and Froudeana.
To mock his supervisor Johann Illingworth, he invented a parasitic mymarid wasp, Shillingsworthia shillingsworthi, which he described as an ephemeral creature lacking a head, abdomen, or mandibles and found only in “the chasms of Jupiter” — in other words, a nonentity. He called it “an airy species whose flight cannot be followed except by the winged mind.”
He understood even women through entomology — one of his privately printed works describes a new species of human, Homo perniciosus, known only from the female sex:
Abnormal female (loveless, without offspring); heart functionless; mammae aborted; psychology novel (as supposed) but artificial; gay, high-coloured, feral, brass-cheeked, shape lovely like Woman but nature hard (selfless, thoughtless, proud, unsympathetic, irresponsible, aggressive, irritant, insensible, luxurious, pugnacious, over-active, inquisitive, mischievous, voracious and even carnivorous; antagonistic, ungentle, immodest, critical, competitive, poisonous); conduct unstable (even inclined to treachery), the lips compressed, body strong. Everywhere but rare in natural habitat.
He was prickly, but he was dedicated — he published much of his work at his own expense, and many of his type specimens are retained today by the Queensland Museum. “Research is a labour of love,” he wrote. “Strange then to find it all done nowadays as a labour of wages! Must love, too, be a matter of cash?”
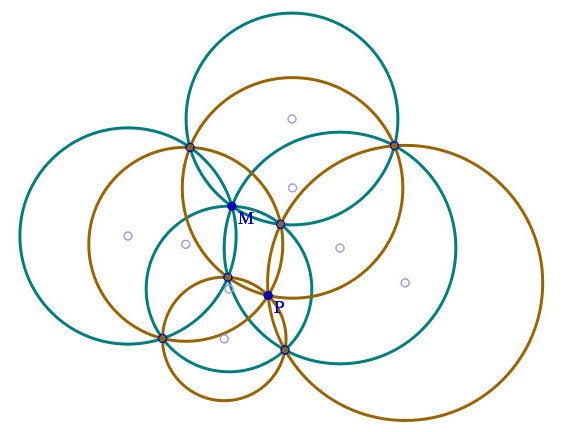
Let four circles (blue) pass through a single point, M. Each pair of these circles intersect at a second point (pink). Each three of the four blue circles will have three pink points among them; these trios of pink points define four new circles (brown), which intersect in a single point, P.
If we start with five circles passing through a single point M, then we can apply the procedure above to each subset of four of them. This will produce five points P that all lie on a single circle.
If we start with six circles that all pass through a single point M, then each subset of five of them defines a new circle, as we’ve just seen. These six new circles all pass through a single point.
Remarkably, this pattern continues forever. It was discovered by the English geometer William Kingdon Clifford.

Arrange cards with values ace through 9 in a row, in counting order, with the ace on the left.
Take up a card from one end of the row — left or right, your choice.
Do this twice more, each time taking up either the leftmost or the rightmost card in the remaining row.
When you have three cards, add their values, divide the total by six, and call the result n. Count the cards that remain on the table from left to right.
The card in the nth position will be the 4.

Alexander Graham Bell kisses his daughter Daisy inside a tetrahedral kite, October 1903.
Bang’s theorem holds that the faces of a tetrahedron all have the same perimeter only if they’re congruent triangles. Also, if they all have the same area, then they’re congruent triangles.
Buckminster Fuller proposed establishing a floating tetrahedron in San Francisco Bay called Triton City (below). It would have been assembled from modules, starting with a floating “neighborhood” of 5,000 residents, with an elementary school, a supermarket and a few specialty shops. Three to six neighborhoods would form a town, and three to seven towns would form a city. At each stage the corresponding infrastructure would be added: schools, civic facilities, government offices, and industry. A full-sized city might accommodate 100,000 people in a single building. He envisioned an even larger tetrahedron, with a million citizens, for Tokyo Bay.
The moral of Fuller’s 1975 book Synergetics was “Dare to be naïve.”

The square root of 2 is 1.41421356237 … Multiply this successively by 1, by 2, by 3, and so on, writing down each result without its fractional part:
![]()
Beneath this, make a list of the numbers that are missing from the first sequence:

The difference between the upper and lower numbers in these pairs is 2, 4, 6, 8 …
From Roland Sprague, Recreations in Mathematics, 1963.

“Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily, so that no two shall walk twice abreast.”
The Rev. Thomas Penyngton Kirkman posed this query innocently in The Lady’s and Gentleman’s Diary in 1850. It’s trickier than it looks — though seven solutions are possible, they’re difficult to discover by trial and error. Here’s one:
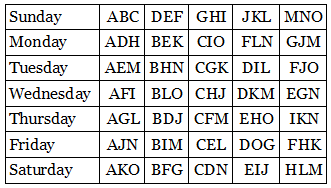
Each letter appears once in each row, but no two letters share a cell more than once. The problem’s simplicity made it popular among Victorian amateur mathematicians, and Kirkman later complained that it had eclipsed his more serious work — though he took pains to dispute James Joseph Sylvester’s claim to have invented the problem himself.
Do such problems generally have solutions? Surprisingly, the answer remained unknown until just last January, when Oxford mathematician Peter Keevash showed that the answer is yes if certain basic requirements are met. Keevash’s result was “a bit of an earthquake as far as design theory is concerned,” said Cambridge mathematician Timothy Gowers.
Now that the schoolgirl problem is under control, a related challenge has taken its place. If 20 golfers want to arrange themselves into different foursomes on five successive days, is it possible to plan the groups so that each golfer plays no more than once with any other golfer? Formally the “social golfer problem” remains unsolved — though tournament organizers work out individual solutions every day.
(Thanks, Martha.)
Divide the number 999,999,999,999,999,999,999,998,999,999,999,999,999,999,999,999 into 1 and express the result as a decimal expansion, and you’ll find the Fibonacci sequence presented in tidy 24-digit strings:

(Thanks, David.)

Amateur magician Oscar Weigle invented this surprising effect in 1949. Assemble a deck of 20 playing cards, 10 red and 10 black, in strictly alternating colors. Hold this deck under a table. Now turn over the top two cards as one, place them on top, and cut the deck. Repeat this procedure as many times as you like — turn two, cut, turn two, cut. When you’ve finished, the deck will contain an unknown number of reversed cards, distributed randomly.
Now, still holding the deck under the table, shift the top card to the bottom, then turn over the next card and place it on the table. Do this repeatedly — shift a card to the bottom, then reverse the next card and put it on the table — continuing until you’ve put 10 cards on the table. Surprisingly, these cards are sorted by color — the face-up cards are of one color, and the face-down ones are of the other.
You’re still holding 10 cards under the table. Divide these into two stacks and weave them together under the table randomly. Do this as many times as you like — divide the 10 cards into two groups and merge them together however you like, so long as no card is turned upside down. Turn over the packet and shuffle it in the same way a few more times. Give it a final cut if you like.
Now deal these cards out as before: Shift the top card to the bottom, reverse the next card and put it on the table. Like the first group, this one will sort itself by color, with one color face up and the other face down.