Until 1911, the U.S. House of Representatives grew along with the country. Accordingly, when the 1880 census showed an increase in population, C.W. Seaton, chief clerk of the census office, worked out apportionments for all House sizes between 275 and 350, in order to see which states would get the new seats.
He was in for a surprise. The method was straightforward: Take the total U.S. population and divide it by the proposed number of seats in the House, rounding all fractions down. This would dispose of most of the seats; any leftover seats would be awarded to the states whose fractional remainders had been highest. But Seaton discovered an oddity:
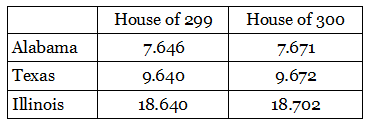
If the House had 299 seats, Alabama would get 8 representatives (because its remainder, .646, was higher than that of Texas or Illinois). But if the House had 300 seats it would get only 7 (the extra representative would now go to Illinois, whose remainder had surpassed Alabama’s). The problem is that the “fair share” of a large state increases more quickly than that of a small state.
Seaton called this the Alabama paradox. A related problem is the population paradox: If the method above had been used in 1901 to reallocate 386 seats in the House, Virginia would have lost a seat to Maine even though the ratio of their populations had increased from 2.67 to 2.68:
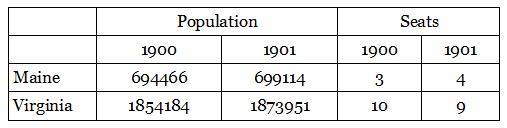
Here, even though the size of the House has not changed, a fast-growing state receives fewer representatives than a slow-growing one.
In 1982 mathematicians Michel Balinski and Peyton Young showed that if each party gets one of the two numbers closest to its fair share of seats, then any system of apportionment will run into one of these paradoxes. The solution, it seems clear, is to start cutting legislators into pieces.
(These data are from Hannu Nurmi’s Voting Paradoxes and How to Deal With Them, 1999. Balinski and Young’s book is Fair Representation: Meeting the Ideal of One Man, One Vote.)