David Hume argued that reports of miracles can never be credited, because the weight of human experience must always favor a more natural explanation. “Nothing is esteemed a miracle, if it ever happen in the common course of nature. It is no miracle that a man, seemingly in good health, should die on a sudden: because such a kind of death, though more unusual than any other, has yet been frequently observed to happen. But it is a miracle, that a dead man should come to life; because that has never been observed in any age or country. There must, therefore, be a uniform experience against every miraculous event, otherwise the event would not merit that appellation.”
The sun is said to have danced in the sky in 1917. Well, which is more likely, that such an extraordinary event actually occurred, or that it was really a mass hallucination, an optical illusion, or any of a hundred more familiar explanations? A miracle, a suspension of natural law, is always the least likely possibility, so as rational creatures we must always reject it.
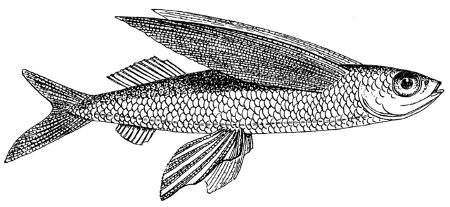
But Alfred Russel Wallace objected, “Such a simple fact as the existence of flying fish could never be proved, if Hume’s argument is a good one; for the first man who saw and described one, would have the universal experience against him that fish do not fly, or make any approach to flying, and his evidence being rejected, the same argument would apply to the second, and to every subsequent witness.”
Hume’s argument, he said, was “radically fallacious,” because if it were sound “no perfectly new fact could ever be proved, since the first and each succeeding witness would be assumed to have universal experience against him.” Who’s right?





