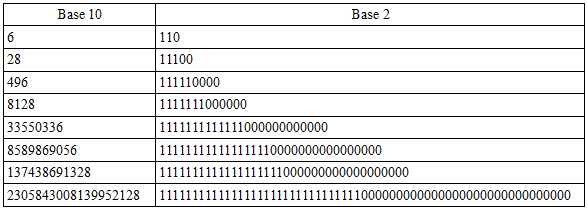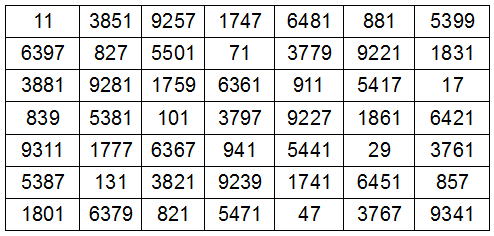
Back in 2010 I posted a prime magic square created by a prison inmate and published anonymously in the Journal of Recreational Mathematics. The same prisoner composed the 7×7 square above, which has some remarkable properties of its own:
- Here again every cell is prime.
- The numbers in each row, column, and the two main diagonals add to the magic constant of 27627.
- That same constant, 27627, is the sum of each broken diagonal (that is, each pair of parallel diagonals that include seven numbers, for example 3881 + 827 + 9257 + 5471 + 1741 + 29 + 6421).
- If the units digit is removed from each number (changing 9341 to 934, 6367 to 636, etc.), then it remains a pandiagonal magic square, with all the properties mentioned above for the primes.
Both squares appeared in the October 1961 issue of Recreational Mathematics Magazine — editor Joseph S. Madachy noted that they had been “sent to Francis L. Miksa of Aurora, Illinois from an inmate in prison who, obviously, must remain nameless.”
It’s not clear to me why the prisoner shouldn’t get credit for this work, whatever his crime — presumably he created both squares while working alone and without tools or references, a remarkable achievement. If I learn any more I’ll post it here.