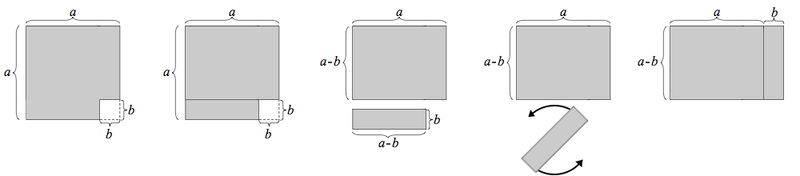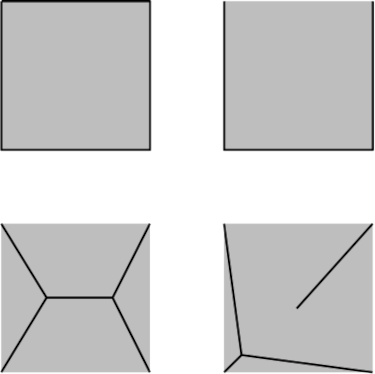
A creature living in the plane can’t see through a unit square — the square’s four line segments block its line of sight from any angle. Is there a way to achieve the same result using fewer building materials? Removing one of the square’s sides does the job — this requires only 3 units of line segment and still prevents anyone from seeing across the square’s area. The arrangement at lower left does better still, requiring only about 2.732 units. And the one at lower right requires only about 2.639 units.
Is that the shortest possible opaque set for the square? Possibly — but no one has been able to prove it.