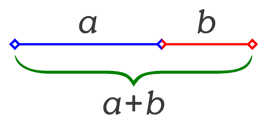
Do men have more sisters than women do? Intuitively it seems they must. In a family with two children, a boy and a girl, the boy has a sister but the girl doesn’t. In a family with four children, two boys and two girls, each boy has two sisters but each girl has one. It seems inevitable that, on average, men must have more sisters than women.
But it isn’t true. There are four possible two-child families, all equally likely: BB, BG, GB, GG. Half of the children in these families have a sibling of the same sex, and half have a sibling of the opposite sex. This observation can be extended to larger families. So men have the same number of sisters as women.
Cut the Knot has a good discussion of the statistics, including a javascript simulator.