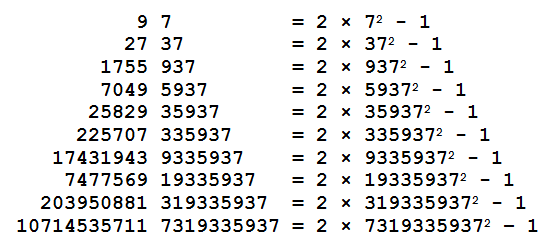
Discovered by J.A.H. Hunter.
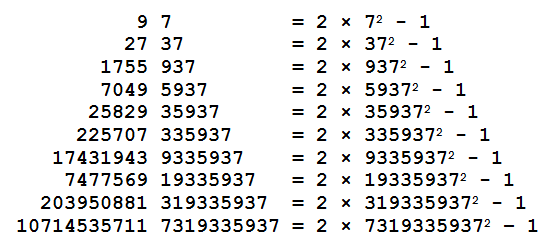
Discovered by J.A.H. Hunter.
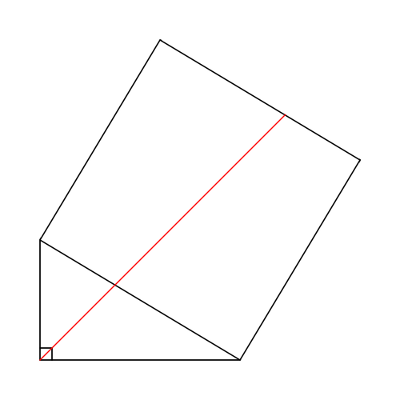
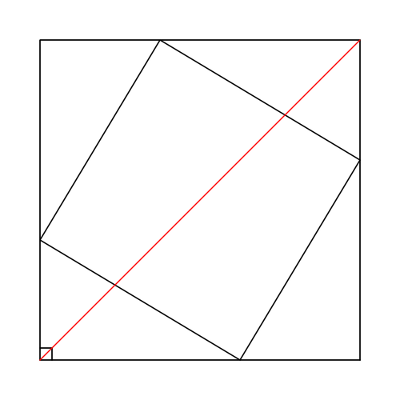
A line that bisects the right angle in a right triangle also bisects a square erected on the hypotenuse.
Proof:

If a second is defined by reference to the rotation of the earth on its axis, i.e. as 1/60 of 1/60 of 1/24 of the time between 2 identical positions of the Greenwich meridian relatively to the fixed stars, then, if the earth rotated 10 times more slowly than it does now, it would be possible to run 10 yds. in a second, instead of only a yard as now, and a second would be 10 times longer than it is now; but if cinema machines still moved as fast as they do now, it would still be quite impossible for any one to see a succession of static pictures instead of a moving one. Don’t we mean by a second the length of time which is now 1/60 of 1/60 of 1/24 of the time between etc.?
— G.E. Moore, Commonplace Book, 1962
On Jan. 18, 1897, California farmer George Jones bought a quantity of livestock feed from Henry B. Stuart of San Jose. As security he signed a $100 promissory note that bore 10 percent interest per month, compounded monthly.
They had agreed that Jones would pay the debt in three months, but the note had run for almost 25 years when Stuart got tired of waiting and told his lawyer to sue. Judge J.R. Welch of the Superior Court of Santa Clara entered this judgment on March 6, 1922:
“Wherefore, by virtue of the law and the facts, it is Ordered, Adjudged and Decreed that said Plaintiff have and recover from said Defendant the sum of $304,840,332,912,685.16 with interest thereon at the rate of 7% per annum until paid, together with the further sum of $50.00 Plaintiff’s attorney’s fees herein with interest thereon at the rate of 7% per annum until paid.”
That’s $304 trillion, “more money than there is in the world, outside of Russia,” the New York Tribune reported drily. Jones paid $19.69 and filed for bankruptcy.
In 1980, Colorado math teacher William J. O’Donnell was explaining that
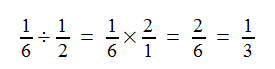
when a student noted that
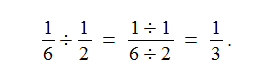
“My immediate reaction was that this student had stumbled onto a special case where this algorithm worked,” O’Donnell wrote in a letter to Mathematics Teacher. “Later, a couple of minutes of work revealed that this technique works for all fractions. Let a, b, c, and d be integers. Then
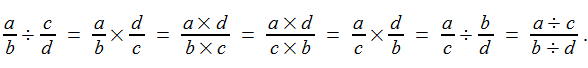
“Whereas this method can be conveniently applied on occasion, it does not offer the student much advantage when c does not divide a and d does not divide b.”
Darth Vader is piloting a barge to Salt Lake City to give a workshop on evildoing. Suddenly he finds himself approaching a crumbling brick aqueduct, at the foot of which is a basket of adorable kittens. He struggles to stop the barge, but it’s too late. The terrified kittens mew piteously, but they’re too weak to escape. Inexorably, implacably, the barge floats out directly over the basket. What happens?
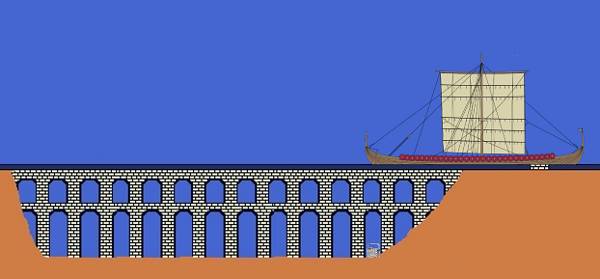
Nothing happens. The barge displaces its weight in water, so there’s no additional load on the aqueduct.
The workshop is a great success.
Let the peal of a gong be heard in the last half of a minute, a second peal in the preceding 1/4 minute, a third peal in the 1/8 minute before that, etc. ad infinitum. … Of particular interest is the following puzzling case. Let us assume that each peal is so very loud that, upon hearing it, anyone is struck deaf — totally and permanently. At the end of the minute we shall be completely deaf (any one peal being sufficient), but we shall not have heard a single peal! For at most we could have heard only one of the peals (any single peal striking one deaf instantly), and which peal could we have heard? There simply was no first peal.
— Jose Benardete, Infinity: An Essay in Metaphysics, 1964
Various writers throughout the 19th century confidently reported that they’d found the true and exact value of π. Unfortunately, they all gave different answers. In 1977 DePauw University mathematician Underwood Dudley tried to make sense of this by compiling 50 of their pronouncements:
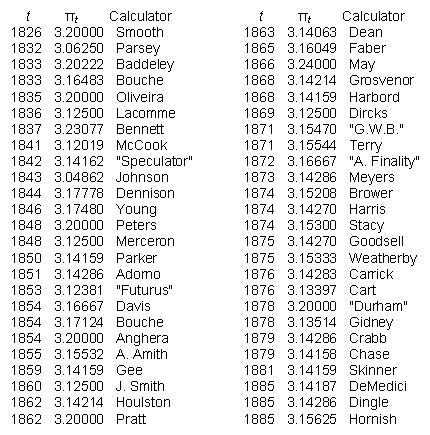
He concluded that π is decreasing. The best fit is πt = 4.59183 – 0.000773t, where t is the year A.D. — it turns out we passed 3.1415926535 back in 1876 and have been heading downward ever since.
And that means trouble: “When πt is 1, the circumference of a circle will coincide with its diameter,” Dudley writes, “and thus all circles will collapse, as will all spheres (since they have circular cross-sections), in particular the earth and the sun. It will be, in fact, the end of the world, and … it will occur in 4646 A.D., on August 9, at 4 minutes and 27 seconds before 9 p.m.”
There is some good news, though: “Circumferences of circles will be particularly easy to calculate in 2059, when πt = 3.”
(Underwood Dudley, “πt,” Journal of Recreational Mathematics 9:3, March 1977, p. 178)

Andy fires a shot at the goal, but it’s deflected by his opponent Bill. If Bill had not reached the ball, it would have struck Charlie, Andy’s teammate. Roberto Casati asks, “Should Bill get credit for the save?”
He: Not quite. After all, the ball was not going to score anyway; it would have hit Charlie’s body.
She: But neither would it be right to say that anything happened thanks to Charlie. After all, Charlie did nothing.
He: But then who is responsible for spoiling Andy’s shot?
“Cases like this one are indicative of a deep conceptual tension,” Casati writes. “I am walking in the rain. My umbrella is open and I am wearing a hat, so my head is not getting wet. But why is that so? It’s not because of the umbrella, because I’m wearing my hat. And it’s not because of my hat, for I have an umbrella.”
From Casati’s excellent book Insurmountable Simplicities. See also In the Dark.