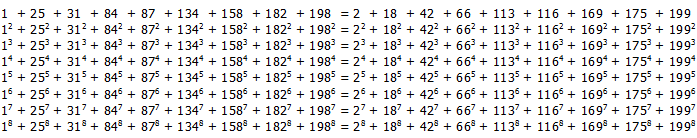1/473684210526315789 = 0.0000000000000000021111111111111111132222222222222 22224333333333333333335444444444444444446555555555555555557666666666666666 66877777777777777777988888888888888889100000000000000000211111111111111111 32222222222222222243333333333333333354444444444444444465555555555555555576 66666666666666668777777777777777779888888888888888891000000000000000002111 11111111111111322222222222222222433333333333333333544444444444444444655555 55555555555576666666666666666687777777777777777798888888888888888910000000 00000000002111111111111111113222222222222222224333333333333333335444444444 44444444655555555555555555766666666666666666877777777777777777988888888888 88888910000000000000000021111111111111111132222222222222222243333333333333 33335444444444444444446555555555555555557666666666666666668777777777777777 77988888888888888889100000000000000000211111111111111111322222222222222222 43333333333333333354444444444444444465555555555555555576666666666666666687 77777777777777779888888888888888891000000000000000002111111111111111113222 22222222222222433333333333333333544444444444444444655555555555555555766666 66666666666687777777777777777798888888888888888910000000000000000021111111 11111111113222222222222222224333333333333333335444444444444444446555555555 55555555766666666666666666877777777777777777988888888888888889100000000000 00000021111111111111111132222222222222222243333333333333333354444444444444 44446555555555555555557666666666666666668777777777777777779888888888888888 89100000000000000000211111111111111111322222222222222222433333333333333333 54444444444444444465555555555555555576666666666666666687777777777777777798 88888888888888891000000000000000002111111111111111113222222222222222224 ...
(Thanks, William.)