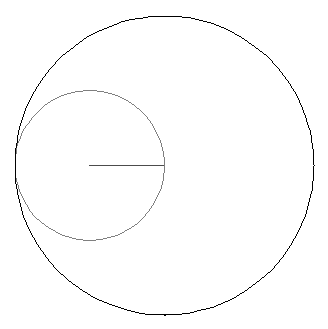
Suppose we set a small circle rolling around the interior of a large circle of twice its diameter. If we follow a point on the small circle, what pattern will it draw?

Suppose we set a small circle rolling around the interior of a large circle of twice its diameter. If we follow a point on the small circle, what pattern will it draw?
By Royal V. Heath:
12 + 43 + 65 + 78 = 87 + 56 + 34 + 21
That’s not terrifically impressive on its face. But:

At the start of her career, NIH immunologist Polly Matzinger disliked writing in the passive voice and felt too insecure to adopt the first person. So she listed her dog, Galadriel Mirkwood, as a coauthor and wrote as “we.”
Their paper was published in 1978 in the Journal of Experimental Medicine. When the editor learned Galadriel’s species, he barred Matzinger from his pages for the rest of his life.
Do men have more sisters than women do? Intuitively it seems they must. In a family with two children, a boy and a girl, the boy has a sister but the girl doesn’t. In a family with four children, two boys and two girls, each boy has two sisters but each girl has one. It seems inevitable that, on average, men must have more sisters than women.
But it isn’t true. There are four possible two-child families, all equally likely: BB, BG, GB, GG. Half of the children in these families have a sibling of the same sex, and half have a sibling of the opposite sex. This observation can be extended to larger families. So men have the same number of sisters as women.
Cut the Knot has a good discussion of the statistics, including a javascript simulator.

If I have two children, there’s a 50 percent chance that I’ll have a boy and a girl.
But if I have four children, the chance that I’ll have an equal number of boys and girls drops to 6 in 16, or 37.5 percent.
This trend continues — as the number of offspring rises, the chance of having precisely the same number of boys and girls drops:
2 children: 50 percent
4 children: 37.5 percent
8 children: 27.34375 percent
16 children: 19.6380615 percent
32 children: 13.9949934 percent
64 children: 9.9346754 percent
128 children: 7.0386092 percent
This is worrying. Does it mean that in a large population Jacks might drastically outnumber Jills?
No. As the population grows, the distribution assumes the shape of a normal bell curve concentrated near 1/2. So while the chance of precise parity drops, the chance that a large population will have approximately equal numbers of girls and boys actually increases, as we’d expect.
The golden mean is quite absurd;
It’s not your ordinary surd.
If you invert it (this is fun!),
You’ll get itself, reduced by one;
But if increased by unity,
This yields its square, take it from me.
— Paul S. Bruckman, The Fibonacci Quarterly, 1977
Bach’s “crab canon” rendered as a Möbius strip:
Bach and Handel were both blinded by the same oculist, John Taylor, “the poster child for 18th-century quackery,” according to University of Wisconsin ophthalmologist Daniel Albert. Bach probably died of a post-operative infection; Handel wrote the lyrics to Samson (“Total eclipse! No sun, no moon! / All dark amidst the blaze of noon!”) after Taylor’s botched cataract surgery.
Random Möbius anecdote: In 1957, B.F. Goodrich patented a half-twisted conveyor belt for carrying hot material such as cinders and foundry sand, “thereby permitting each face of the belt to cool during one half of the operating period.”

What would happen if you jumped into a tunnel that passed through the center of the earth? If you encountered no air resistance, dinosaurs, Mad Hatters, or Morlocks, you’d accelerate until you passed through the center at 18,000 mph, then slow as you ascended through the opposite hemisphere. At the far end you’d have just time to tip your hat to the surprised antipodeans before you fell home again, and you’d continue oscillating like this forever.
“If this shaft had its starting-point on one of the mountain plateaux of South America at an elevation of seven thousand feet,” wrote Camille Flammarion in 1909, “and if it issued at the sea-level at the other side, a man who had fallen into the shaft would arrive at the antipodes still travelling at such a speed that the spectators would see this strange projectile shot to a height of seven thousand feet into the air.”
On the other hand, if our straight tunnel connected two points that were not precise antipodes, then we could install a train powered by gravity — it would roll “downhill” on the first part of its journey, and momentum would carry it through the second (again neglecting air resistance and friction). Curiously, in all these cases the total trip would take the same length of time — about 42 minutes.

Discovered by J.A.H. Hunter.