Socrates likes company. He wants to eat only if Plato wants to eat.
But Plato is angry at Socrates. He wants to eat only if Socrates does not want to eat.
Does Socrates want to eat?
(From Buridan’s Sophismata.)
Socrates likes company. He wants to eat only if Plato wants to eat.
But Plato is angry at Socrates. He wants to eat only if Socrates does not want to eat.
Does Socrates want to eat?
(From Buridan’s Sophismata.)
Suppose there were an experience machine that would give you any experience you desired. Superduper neuropsychologists could stimulate your brain so that you would think and feel you were writing a great novel, or making a friend, or reading an interesting book. All the time you would be floating in a tank, with electrodes attached to your brain. Should you plug into this machine for life, preprogramming your life’s experiences? If you are worried about missing out on desirable experiences, we can suppose that business enterprises have researched thoroughly the lives of many others. You can pick and choose from their large library or smorgasbord of such experiences, selecting your life’s experiences for, say, the next two years. After two years have passed, you will have ten minutes or ten hours out of the tank, to select the experiences of your next two years. Of course, while in the tank you won’t know that you’re there; you’ll think it’s all actually happening. … Would you plug in?
— Robert Nozick, Anarchy, State, and Utopia, 1974
10102323454577 is the smallest 14-digit prime number that follows the rhyme scheme of a Shakespearean sonnet (ababcdcdefefgg).
(Discovered by Jud McCranie.)
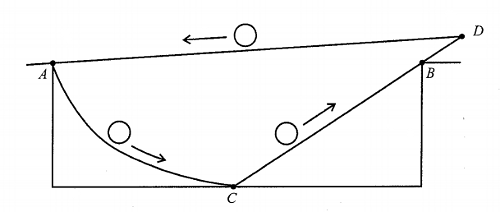
Eric Chandler offered this perpetual-motion scheme for Edward Barbeau’s “Fallacies, Flaws and Flimflam” column in the College Mathematical Journal. Points A and B are at the same height, and C is halfway between them. The ramp AC is a segment of a cycloid, a curve designed to produce the fastest descent under gravity.
A ball released at A rolls down the ramp AC to C covering a greater distance in a shorter time than it would have had it rolled down BC to C. The relation Velocity = Distance/Time thus implies that the ball arrives at C with greater velocity than it would have had it rolled down BC. This added velocity enables the ball to roll from C up to and past B to a point D a little farther along. It then returns to A along the inclined ramp DA to repeat the cycle endlessly.
Where is the error?
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999989999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999 is prime.
In probability theory, the formula for the Poisson distribution is
Pm(n) = mne–m/n!
Pleasingly, the mnemonic for this is mnemonic: “m to the n, e to the –m over n factorial.” Arguably the factorial sign even resembles an inverted i.
Now we just need a way to remember that …
(From M.H. Greenblatt, Mathematical Entertainments, 1965.)
There was Diodorus Chronos, a most acute and subtle reasoner. He proved there was no such thing as motion. A body must move either in the place where it is or in the place where it is not. Now, a body cannot be in motion in the place where it is stationary, and cannot be in motion in the place where it is not. Therefore, it cannot move at all. …
Diodorus was brought up roundly by another densely practical intelligence. Having dislocated his shoulder, he sent for a surgeon to set it. ‘Nay,’ said the practitioner, doubtful, perhaps, whether so subtle an intelligence might not euchre him out of his fee by some logical ingenuity, ‘your shoulder cannot possibly be put out at all, since it cannot be put out in the place in which it is, nor yet in the place in which it is not.’
— “Some Famous Paradoxes,” The Illustrated American, Nov. 1, 1890

A correspondent at Princeton College sent this conundrum to Sam Loyd:
“Supposing that a bird weighing one ounce flies into a box with only one small opening, and without resting continues to fly round and round in the box, would it increase or lessen the weight of the box?”
Loyd said he was open to argument, but “the preponderance of opinion is so overwhelmingly in favor of the weight of the bird being added to that of the box, that it would be difficult to present reasonable argument for the other side, despite of the popular belief that such would be the case. … The bird is heavier than the air and supports itself by striking down upon the air and the power of such strokes would undoubtedly show on the dial the difference in weight between the bird and its displacement of air.”
A related problem from Clark Kinnaird’s Encyclopedia of Puzzles and Pastimes (1946):
“A vagrant who stole three melons weighing three pounds each, came to a bridge which was just strong enough to hold him and six pounds. Without throwing any of the melons across the bridge, how did the vagrant cross the bridge with the melons, none of which touched the bridge?”
Kinnaird’s answer: He juggled them.
1212 + 1388 + 2349 = 4949; 49493 = 121213882349
1287 + 1113 + 2649 = 5049; 50493 = 128711132649
1623 + 2457 + 1375 = 5455; 54553 = 162324571375
1713 + 2377 + 1464 = 5554; 55543 = 171323771464
3689 + 1035 + 2448 = 7172; 71723 = 368910352448