A rail one mile long is lying on the ground. If you push its ends closer together by a single foot, so that the distance between them is 5279 feet rather than 5280, how high an arc will the rail make?
Science & Math
Misc
- Dorothy Parker named Alexander Woollcott’s apartment “Wit’s End.”
- Can you look at something and imagine it at the same time?
- 36850 = (36 + 8) × 50
- AGNOSTIC is an anagram of COASTING.
- “The errors of a man are what make him really lovable.” — Goethe
Skyline Trouble

In June 1978, a Princeton engineering student called structural engineer William LeMessurier with some worrying calculations. LeMessurier’s new Citicorp Tower, which had opened the previous year, was vulnerable to quartering winds — winds that blew from a 45-degree angle. On investigating, LeMessurier found also that the welded joints he had specified had been replaced with weaker bolted joints during construction. This meant that a strong wind could shear the bolts and topple a 59-story building into midtown Manhattan.
With hurricane season approaching, welders worked from 8 p.m. to 4 a.m. every night, reinforcing the building’s joints, and the Red Cross worked out an evacuation plan for the surrounding neighborhood. Because of a press strike at the time, many of these details came to light only 20 years later.
That year’s Hurricane Ella actually bore down on New York as the workers were finishing the job, but the storm veered out to sea before reaching the city. The welding was completed in October, and it’s now estimated that a storm strong enough to rock the tower will occur only once every 700 years.
Tock

How fast does time pass? We have no way to measure this. We can reply, helplessly, that it passes at one second per second, but this is not a rate of change — 1 second divided by 1 second is 1. Not 1 of anything, just 1.
“‘One’ can be an answer, right or wrong, to the questions ‘How many children had Lady Macbeth?’, ‘How many Gods are there?’, and ‘How many minutes do sixty seconds make?’,” writes Notre Dame philosopher Peter van Inwagen. “‘One’ can never be an answer, not even a wrong one, to any other sort of question — including those questions that ask ‘how fast?’ or ‘at what rate?’ Therefore, if time is moving, it is not moving at any rate or speed.”
(From his Metaphysics, 2002.)
Ceramic Geometry
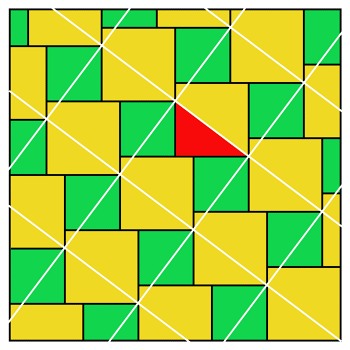
This tiling pattern is sometimes referred to as Pythagorean because it can be construed to prove the Pythagorean theorem.
The red area is a right triangle. The square of its shorter side is equivalent to a green square, and the square of its longer side is equivalent to a yellow square.
One green and one yellow square can be cut up and reassembled to fit into one of the canted white squares, which is equivalent to the square of the red triangle’s hypotenuse. Hence a2 + b2 = c2.
Keeping Things Interesting

Each year, when the last flight of the summer field season departs the U.S. research station at the South Pole, the remaining staff gather to watch The Thing.
The next flight won’t arrive for eight months.
Time and Again
Imagine that I first walk through Divinity Avenue, and then imagine that the powers governing the universe annihilate ten minutes of time with all that it contained, and set me back at the door of this hall just as I was before the choice was made. Imagine then that, everything else being the same, I now make a different choice and traverse Oxford Street. You, as passive spectators, look on and see the two alternative universes,–one of them with me walking through Divinity Avenue in it, the other with the same me walking through Oxford Street. Now, if you are determinists you believe one of these universes to have been from eternity impossible: you believe it to have been impossible because of the intrinsic irrationality or accidentality somewhere involved in it. But looking outwardly at these universes, can you say which is the impossible and accidental one, and which the rational and necessary one? I doubt if the most ironclad determinist among you could have the slightest glimmer of light on this point. In other words, either universe after the fact and once there would, to our means of observation and understanding, appear just as rational as the other.
— William James, “The Will to Believe,” 1896
Healthcare Reform

The statement “You will recover from this illness” is either true or false. If it’s true, then it has been true for all eternity, and you’ll recover whether you summon a doctor or not.
If the statement is false, then it has always been false, and you will not recover even with a doctor’s aid.
So there is no point in calling a doctor.
(From Cicero’s De Fato.)
A Good Man

Should other species be regarded as human? In 1779 Lord Monboddo proposed that orangutans should: They walk upright, use weapons, form societies, build shelters, and behave with “dignity and composure.” “If … such an Animal be not a Man, I should desire to know in what the essence of a Man consists, and what it is that distinguishes a Natural Man from the Man of Art?”
Thomas Love Peacock mocked this view in his 1817 novel Melincourt, in which a civilized orangutan (“Sir Oran Hout-ton”) is elected to Parliament. And an anonymous wag objected even to the satire:
The author of a novel lately written,
Entitled “Melincourt,”
(‘Tis very sweet and short),
Seems indeed by some wondrous madness bitten,
Thinking it good
To take his hero from the wood:
And though I own there’s nothing treasonable
In making ouran-outangs reasonable,
I really do not think he should
Go quite the length that he has done,
Whether for satire or for fun,
To make this creature an M.P.
As if mankind no wiser were than he.
However, those who’ve read it
Must give the author credit
For skill and ingenuity,
Although it have this monstrous incongruity.
But today Monboddo’s view is on the ascendancy. In Rattling the Cage (2014), Harvard legal scholar Steven M. Wise argues that orangutans — as well as chimpanzees, bonobos, elephants, parrots, dolphins, and gorillas — deserve legal personhood. “Ancient philosophers claimed that all nonhuman animals had been designed and placed on this earth just for human beings,” he writes. “Ancient jurists declared that law had been created just for human beings. Although philosophy and science have long since recanted, the law has not.”
Heavenly Form
The U.S. Customs Service received an odd bit of paperwork on July 24, 1969:

All three Apollo 11 astronauts signed the form, which was filed at the Honolulu airport on the day they splashed down.
“Yes, it’s authentic,” NASA spokesperson John Yembrick told Space.com. “It was a little joke at the time.”
See Business Trip and Space Bills.
