- Richard Gere’s middle name is Tiffany.
- Where does the hinterland begin?
- WORLD CUP TEAM is an anagram of TALCUM POWDER.
- log 237.5812087593 = 2.375812087593
- “Why is it that something can be transparent green but not transparent white?” — Wittgenstein
Science & Math
Round Trip
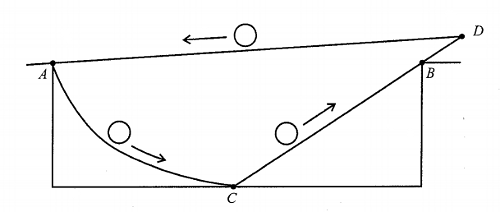
Eric Chandler offered this perpetual-motion scheme for Edward Barbeau’s “Fallacies, Flaws and Flimflam” column in the College Mathematical Journal. Points A and B are at the same height, and C is halfway between them. The ramp AC is a segment of a cycloid, a curve designed to produce the fastest descent under gravity.
A ball released at A rolls down the ramp AC to C covering a greater distance in a shorter time than it would have had it rolled down BC to C. The relation Velocity = Distance/Time thus implies that the ball arrives at C with greater velocity than it would have had it rolled down BC. This added velocity enables the ball to roll from C up to and past B to a point D a little farther along. It then returns to A along the inclined ramp DA to repeat the cycle endlessly.
Where is the error?
Math Notes
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999989999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999999999999999
99999999999999999999999999999999999999999999999999999999999999 is prime.
Unforgettable
In probability theory, the formula for the Poisson distribution is
Pm(n) = mne–m/n!
Pleasingly, the mnemonic for this is mnemonic: “m to the n, e to the –m over n factorial.” Arguably the factorial sign even resembles an inverted i.
Now we just need a way to remember that …
(From M.H. Greenblatt, Mathematical Entertainments, 1965.)
Case Closed
There was Diodorus Chronos, a most acute and subtle reasoner. He proved there was no such thing as motion. A body must move either in the place where it is or in the place where it is not. Now, a body cannot be in motion in the place where it is stationary, and cannot be in motion in the place where it is not. Therefore, it cannot move at all. …
Diodorus was brought up roundly by another densely practical intelligence. Having dislocated his shoulder, he sent for a surgeon to set it. ‘Nay,’ said the practitioner, doubtful, perhaps, whether so subtle an intelligence might not euchre him out of his fee by some logical ingenuity, ‘your shoulder cannot possibly be put out at all, since it cannot be put out in the place in which it is, nor yet in the place in which it is not.’
— “Some Famous Paradoxes,” The Illustrated American, Nov. 1, 1890
The Flying Bird

A correspondent at Princeton College sent this conundrum to Sam Loyd:
“Supposing that a bird weighing one ounce flies into a box with only one small opening, and without resting continues to fly round and round in the box, would it increase or lessen the weight of the box?”
Loyd said he was open to argument, but “the preponderance of opinion is so overwhelmingly in favor of the weight of the bird being added to that of the box, that it would be difficult to present reasonable argument for the other side, despite of the popular belief that such would be the case. … The bird is heavier than the air and supports itself by striking down upon the air and the power of such strokes would undoubtedly show on the dial the difference in weight between the bird and its displacement of air.”
A related problem from Clark Kinnaird’s Encyclopedia of Puzzles and Pastimes (1946):
“A vagrant who stole three melons weighing three pounds each, came to a bridge which was just strong enough to hold him and six pounds. Without throwing any of the melons across the bridge, how did the vagrant cross the bridge with the melons, none of which touched the bridge?”
Kinnaird’s answer: He juggled them.
Math Notes
1212 + 1388 + 2349 = 4949; 49493 = 121213882349
1287 + 1113 + 2649 = 5049; 50493 = 128711132649
1623 + 2457 + 1375 = 5455; 54553 = 162324571375
1713 + 2377 + 1464 = 5554; 55543 = 171323771464
3689 + 1035 + 2448 = 7172; 71723 = 368910352448
Applied Chemistry
When Hitler’s army marched into Copenhagen, Niels Bohr had to decide how to safeguard the Nobel medals of James Franck and Max von Laue, which they had entrusted to him. Sending gold out of the country was almost a capital offense, and the physicists’ names were engraved on the medals, making such an attempt doubly risky. Burying the medals seemed uncertain as well. Finally his friend the Hungarian physicist Georg von Hevesy invented a novel solution: He dissolved the medals in a jar of aqua regia, which Bohr left on a shelf in his laboratory while he fled to Sweden.
When he returned in 1945, the jar was still there. Bohr had the gold recovered, and the Nobel Foundation recast it into two medals.
(Chemist Hermann Mark found a way to escape Germany with his money: He used it to buy platinum wire, which he fashioned into coat hangers. Once he had brought these successfully through customs, he sold them to recover the money.)
Twice Told
Do those, said he, who learn, learn what they know, or what they do not know?
Cleinias had answered Euthydemus that those who learned learn what they do not know; and he put him through a series of questions the same as before.
Do you not know letters?
He assented.
All letters?
Yes.
But when the teacher dictates to you, does he not dictate letters?
To this also he assented.
Then if you know all letters, he dictates that which you know?
This again was admitted by him.
Then, said the other, you do not learn that which he dictates; but he only who does not know letters learns?
Nay, said Cleinias; but I do learn.
Then, said he, you learn what you know, if you know all the letters?
He admitted that.
Then, he said, you were wrong in your answer.
— Plato, Euthydemus
The Two Cultures
Paul Dirac, the British theoretical physicist, has a reputation for being reserved and speaking little. He read E.M. Forster’s A Passage to India, and commented favorably on it. Someone in Cambridge thought the two great men ought to meet. J.G. Crowther recalls that this was arranged. The two men observed each other in long, silent respect. Presently Dirac asked, ‘What happened in the cave?’ ‘I don’t know,’ said Forster, which concluded their conversation.
— Bulletin of the Atomic Scientists, March 1971
