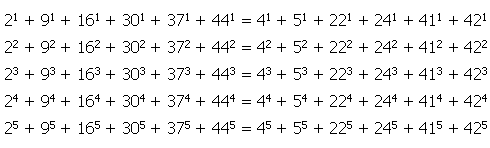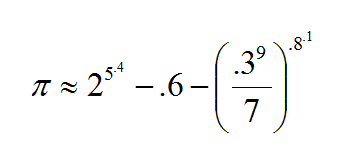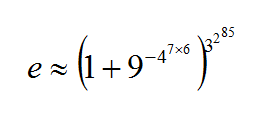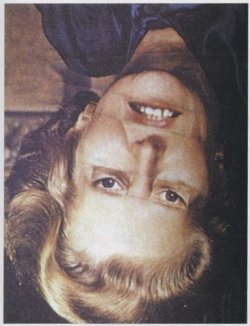
When we look at another person’s face, her eyes and mouth convey the most information about her mood.
Indeed, when a face is inverted we can have trouble recognizing it because we can’t read its expression.
So in 1980 University of York psychologist Peter Thompson tried inverting everything but the eyes and mouth.
Most people can recognize the face at left and assign a mood to it, but they’re often surprised to see it right side up.
“Further research into this illusion might help determine whether face recognition is a serial or parallel process,” Thompson wrote in Perception that summer. “It might even tell us something about Margaret Thatcher.”