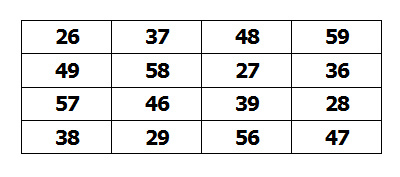
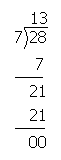Three patricians of the coal yards fared forth on mercy bent, each in his great black chariot. Their overlord, the yard superintendent, had bade them deliver to seven families a total of twenty-eight tons of coal equally divided.
Well out of the yards, each with his first load, Kelly and Burke and Shea paused to discuss the problem of equal distribution — how much coal should each family get?
”Tis this way,’ argued Burke. ”Tis but a bit of mathematics. If there are 7 families an’ 28 tons o’ coal ye divide by 7, which is done as follows: Seven into 8 is 1, 7 into 21 is 3, which makes 13.’ He triumphantly exhibited his figures made with a stubby pencil on a bit of grimy paper:
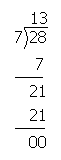
The figures were impressive but Shea was not wholly convinced. ‘There’s a easy way o’ provin’ that,’ he declared. ‘Ye add 13 seven times,’ and he made his column of figures according to his own formula. Then, starting from the bottom of the 3 column, he reached the top with a total of 21 and climbed down the column of 1’s, thus; ‘3, 6, 9, 12, 15, 18, 21, 22, 23, 24, 25, 26, 27, 28.’ ‘Burke is right,’ he announced with finality.
This was Shea’s exhibit:
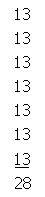
‘There is still some doubt in me mind,’ said Kelly. ‘Let me demonstrate in me own way. If ye multiply the 13 by 7 and get 28, then 13 is right.’ He produced a bit of stubby pencil and a sheet of paper. ”Tis done in this way,’ he said. ‘Seven times 3 is 21; 7 times 1 is 7, which makes 28. ‘Tis thus shown that 13 is the right figure and ye’re both right. Would ye see the figures?’
Kelly’s feat in mathematics was displayed as follows;
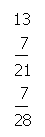
‘There is no more argyment,’ the three agreed, so they delivered thirteen tons of coal to each family.
— Irvin S. Cobb, A Laugh a Day Keeps the Doctor Away, 1923