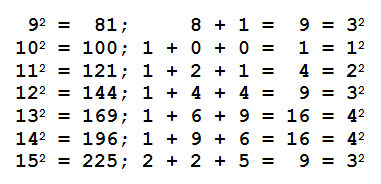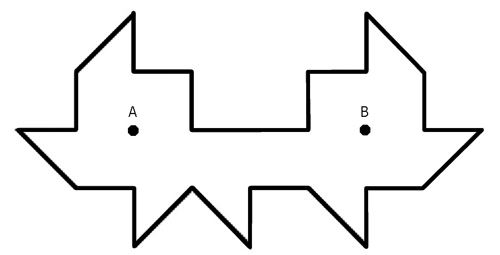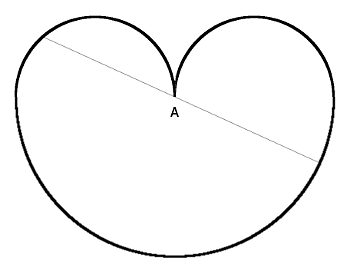
Draw a semicircle and surmount it with two smaller semicircles.
A line drawn through A, at any angle, will divide the perimeter precisely in half.
This probably has some romantic symbolism, but I’m not very good at that stuff.
06/19/2024 Very belated update: This is called the cardioid of Boscovich, after Roger Boscovich, 1711-1787. There’s a proof of the theorem in Alsina and Nelsen, Icons of Mathematics.