
“A universe simple enough to be understood is too simple to produce a mind capable of understanding it.” — Cambridge cosmologist John Barrow

“A universe simple enough to be understood is too simple to produce a mind capable of understanding it.” — Cambridge cosmologist John Barrow
One day while teaching a class at Yale, Shizuo Kakutani wrote a lemma on the blackboard and remarked that the proof was obvious. A student timidly raised his hand and said that it wasn’t obvious to him. Kakutani stared at the lemma for some moments and realized that he couldn’t prove it himself. He apologized and said he would report back at the next class meeting.
After class he went straight to his office and worked for some time further on the proof. Still unsuccessful, he skipped lunch, went to the library, and tracked down the original paper. It stated the lemma clearly but left the proof as an “exercise for the reader.”
The author was Shizuo Kakutani.
Stigler’s Law of Eponymy states that “no scientific discovery is named after its original discoverer.” Examples:
University of Chicago statistics professor Stephen Stigler advanced the idea in 1980.
Delightfully, he attributes it to Robert Merton.
[Bertrand] Russell is reputed at a dinner party once to have said, ‘Oh, it is useless talking about inconsistent things, from an inconsistent proposition you can prove anything you like.’ Well, it is very easy to show this by mathematical means. But, as usual, Russell was much cleverer than this. Somebody at the dinner table said, ‘Oh, come on!’ He said, ‘Well, name an inconsistent proposition,’ and the man said, ‘Well, what shall we say, 2 = 1.’ ‘All right,’ said Russell, ‘what do you want me to prove?’ The man said, ‘I want you to prove that you are the pope.’ ‘Why,’ said Russell, ‘the pope and I are two, but two equals one, therefore the pope and I are one.’
— Jacob Bronowski, The Origins of Knowledge and Imagination, 1979
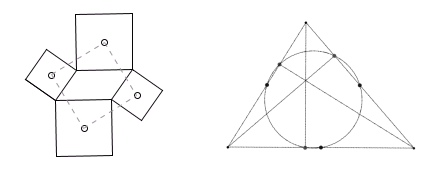
Erect squares on the sides of any parallelogram and their centers will always form a square.
In any triangle, the midpoints of the sides and the feet of the altitudes always fall on a circle.
Write down any natural number, reverse its digits to form a new number, and add the two:
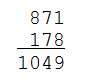
In most cases, repeating this procedure eventually yields a palindrome:
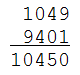
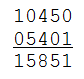
With 196, perversely, it does not — or, at least, it hasn’t in computer trials, which have repeated the process until it produced numbers 300 million digits long.
Is 196 somehow immune to producing palindromes? No one’s yet offered a conclusive proof — so we don’t know.
One threatening morning as Einstein was about to leave his house in Princeton, Mrs. Einstein advised him to take along a hat.
Einstein, who rarely used a hat, refused.
‘But it might rain!’ cautioned Mrs. Einstein.
‘So?’ replied the mathematician. ‘My hair will dry faster than my hat.’
– Howard Whitley Eves, In Mathematical Circles: Quadrants III and IV, 1969
12 = 3 × 4; 56 = 7 × 8
In English, the name of each integer shares a letter with each of its neighbors. ONE shares an O with TWO, TWO shares a T with THREE … and so on to infinity.

In late 1801, Johann Bode, director of the Berlin Observatory, received a curious series of letters from astronomer Hofrath Huth in Frankfort-on-the-Oder. On Dec. 2 Huth had seen something new in the sky, “a star with faint reddish light, round, and admitting of being magnified.” But it wasn’t a star: On subsequent nights he watched it drift slowly to the southwest, growing gradually fainter, and by Jan. 6 it had disappeared. Huth concluded that he was watching an object recede from Earth.
Unfortunately, Bode was busy with other things, and the weather was too cloudy for him to confirm Huth’s observations. Also, the positional data that Huth had provided were somewhat poor.
Huth wasn’t a nut: Among other things, he co-discovered Comet Encke in 1805. And Nature noted later that he had alerted Bode to the object in time for the director to witness it himself if the skies had been clear. But as it happened, Huth was the only one to witness the curious object, whatever it was. And, whatever it was, it has not returned.