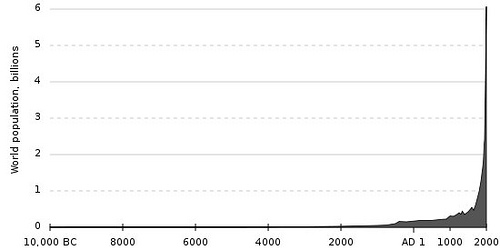
In 1868, 8-year-old Alice Raikes was playing with friends in her London garden when a visitor at a neighbor’s house overheard her name and called to her.
“So you are another Alice,” he said. “I’m very fond of Alices. Would you like to come and see something which is rather puzzling?” He led them into a room with a tall mirror in one corner.
‘Now,’ he said, giving me an orange, ‘first tell me which hand you have got that in.’ ‘The right,’ I said. ‘Now,’ he said, ‘go and stand before that glass, and tell me which hand the little girl you see there has got it in.’ After some perplexed contemplation, I said, ‘The left hand.’ ‘Exactly,’ he said, ‘and how do you explain that?’ I couldn’t explain it, but seeing that some solution was expected, I ventured, ‘If I was on the other side of the glass, wouldn’t the orange still be in my right hand?’ I can remember his laugh. ‘Well done, little Alice,’ he said. ‘The best answer I’ve had yet.’
“I heard no more then, but in after years was told that he said that had given him his first idea for Through the Looking-Glass, a copy of which, together with each of his other books, he regularly sent me.”