Type 120121 into a calculator and you’ll find it’s prime every way you look at it: right side up, upside down (121021), in a mirror (151051), or both (150151).
Science & Math
Math Notes
35 – 32 – 52 = 75 – 72 – 52
Rimshot
A neutron walks into a bar and orders a beer.
“How much do I owe you?” he says.
“For you,” says the bartender, “no charge.”
A Mathematical Limerick
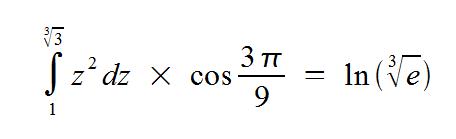
The integral z-squared dz
From one to the cube root of three
Times the cosine
Of three pi over nine
Equals log of the cube root of e.
Math Notes
144648 = 861 × 168 = 492 × 294
185472 = 672 × 276 = 384 × 483
9949716 = 2583 × 3852 = 1476 × 6741
16746912 = 2556 × 6552 = 4473 × 3744
The Goldbach Conjecture
Every even number is the sum of two primes.
Is that true? No one knows. Originally proposed in 1742, it’s been tested as far as 1018, but the jury’s still out.
Live and Let Die
James Bond never really explains why he likes his martinis “shaken, not stirred,” so in 1999 the University of Western Ontario’s biochemistry department decided to find out.
They discovered that a shaken gin martini has stronger antioxidant properties than a stirred one — which would help Bond avoid cardiovascular disease, stroke, and cataracts.
In their writeup for the British Medical Journal, they conclude, “007’s profound state of health may be due, at least in part, to compliant bartenders.”
See also Silly Old Bear.
A Self-Descriptive Number
In the number 6210001000:
- The digit 0 occurs 6 times
- The digit 1 occurs 2 times
- The digit 2 occurs 1 time
- The digit 3 occurs 0 times
- The digit 4 occurs 0 times
- The digit 5 occurs 0 times
- The digit 6 occurs 1 time
- The digit 7 occurs 0 times
- The digit 8 occurs 0 times
- The digit 9 occurs 0 times
See also The Quick Brown Fox …
Math Notes
115132219018763992565095597973971522401 = 139 + 139 + 539 + 139 + 339 + 239 + 239 + 139 + 939 + 039 + 139 + 839 + 739 + 639 + 339 + 939 + 939 + 239 + 539 + 639 + 539 + 039 + 939 + 539 + 539 + 939 + 739 + 939 + 739 + 339 + 939 + 739 + 139 + 539 + 239 + 239 + 439 + 039 + 139
One-Sided Issue

The international symbol for recycling depicts a Möbius strip.
