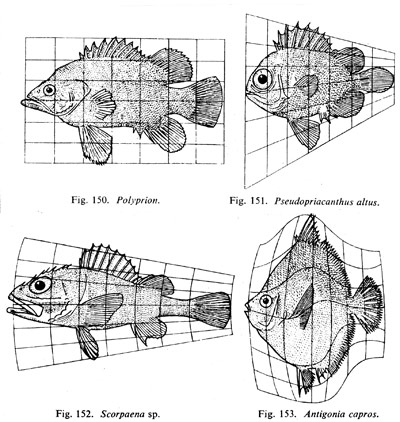
Biologist and mathematician D’Arcy Thompson advanced a strange new idea in his 1917 book On Growth and Form: He found that if you draw the outline of an animal or plant on an ordinary Cartesian grid, and then you put the grid through some mathematical transformation (stretching it, for example, so that its squares become rhombuses), very often the resulting shape is that of a related real creature.
What can that mean? Thompson doesn’t really say. He thought that the biologists of his day overemphasized evolution in explaining the form and structure of living things; he preferred to look for physical and especially mathematical laws. But he didn’t present his ideas as principles that might be tested, so his book has (so far) remained only a notable curiosity.
“This theory cries out for causal explanation, which is something the great man eschewed,” writes zoologist Wallace Arthur. “Perhaps the time is close when comparative developmental genetics will be able to provide such an explanation.”
(Wallace Arthur, “D’Arcy Thompson and the Theory of Transformations,” Nature Reviews Genetics, May 2006, 401-406.)