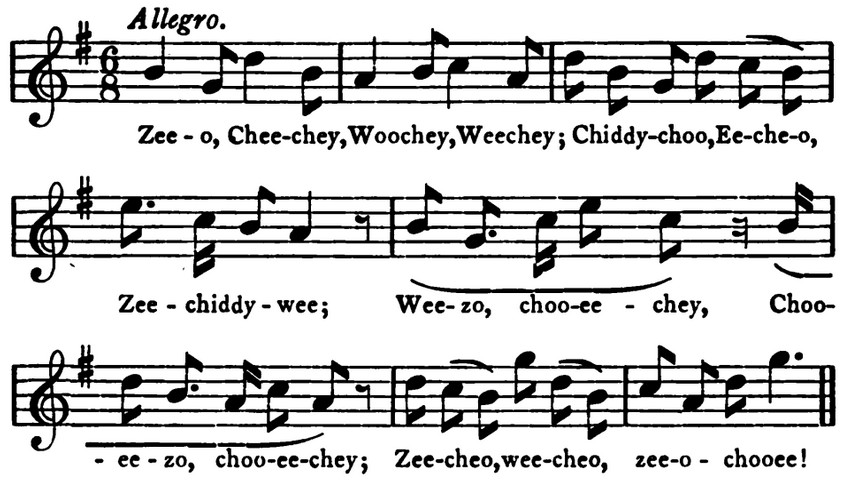
In his 1922 book Songs of the Birds, Oxford zoologist Walter Garstang set out to record birdsongs as musical compositions:
The peculiar quality or timbre of each bird’s voice and the resonance of each sound have been imitated as closely as possible by a selection of human consonants; the composition of the song has been represented by the appropriate repetition, modification, or contrast of selected syllables; the syllabic rendering has been cast in a corresponding rhythm; and round this chosen sequence of syllables a song has been woven to capture something, if possible, of the joy or of the attendant circumstances which form the natural setting of his song.
“I fell in love with my models,” he wrote, “and could not content myself with a purely scientific account of their performances.” He was similarly enraptured by amphibians — the 1951 book Larval Forms collects his poems about marine larvae:
Amblystoma’s a giant newt who rears in swampy waters,
As other newts are wont to do, a lot of fishy daughters:
These Axolotls, having gills, pursue a life aquatic,
But, when they should transform to newts, are naughty and erratic.
His colleague Alister Hardy wrote, “I certainly believe that he gets his ideas across with much greater felicity in these sparkling rhymes than he has done in all his more carefully calculated prose.”
See Bird Songs.