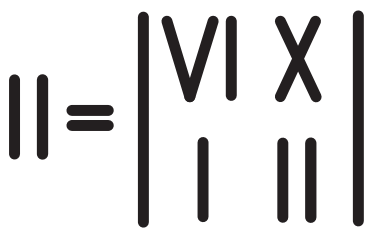What’s the funniest number? Yale physicist Emily Pottebaum proposed the Perceived Specificity Hypothesis, which states that “for nonnegative integers < 100, the funniness of a number increases with its apparent precision." She surveyed 68 acquaintances and found that:
- Among integers divisible by 10, 0 is funniest.
- Odd numbers are consistently funnier than even.
- “Furthermore, the most oddly specific numbers — odd numbers with a degree of specificity of 2 — are the most funny, according to the data presented here.”
The degree of specificity characterizes the distance between an integer and the nearest multiple of 5:
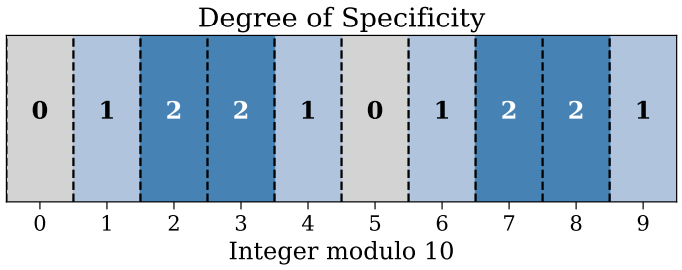
So 3, 7, 13, 17, etc. were judged to be funniest.
“I acknowledge my Ph.D. advisor, who I shall not name out of respect for her academic integrity, for her exasperation upon learning about this study. I thank her for putting up with my antics and plead that she continue to do so until I graduate.”
(E.G. Pottebaum, “What Is the Funniest Number? An Investigation of Numerical Humor,” arXiv preprint, arXiv:2503.24175 [2025].)