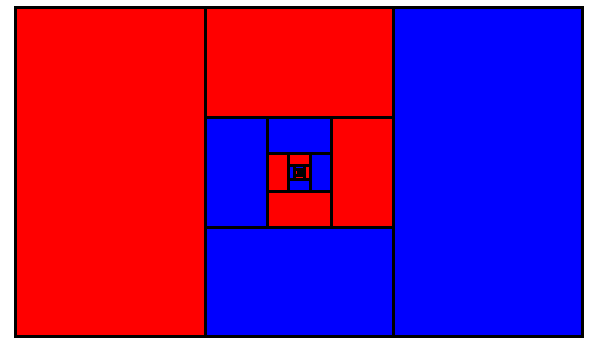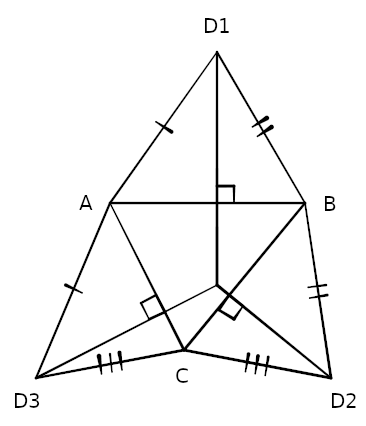
Consider a triangle ABC and three other triangles (ABD1, BCD2, and ACD3) that share common sides with it, and assume that the sides adjacent to any vertex of ABC are equal, as shown. The altitudes of the three outer triangles, passing through D1, D2, and D3 and orthogonal to the sides of ABC, meet in a point.
This can be made intuitive by imagining the figure in three dimensions. Fold each of the outer triangles “up,” out of the page. Their outer vertices will meet at the apex of a tetrahedron. Now if we imagine looking straight down at that apex and folding the sides down again, each of those vertices will follow the line of an altitude (from our perspective) on the way back to its original position, because each follows an arc that’s orthogonal to the horizontal plane and to one of the sides of ABC. The result is the original figure.
(Alexander Shen, “Three-Dimensional Solutions for Two-Dimensional Problems,” Mathematical Intelligencer 19:3 [June 1997], 44-47.)