If you arrange the first 12 primes into exponentiated summands, you get a prime number:
23 + 57 + 1113 + 1719 + 2329 + 3137 = 15148954872646850196557152427604893685308877022260348791 is prime.
(From Fermat’s Library.)
If you arrange the first 12 primes into exponentiated summands, you get a prime number:
23 + 57 + 1113 + 1719 + 2329 + 3137 = 15148954872646850196557152427604893685308877022260348791 is prime.
(From Fermat’s Library.)
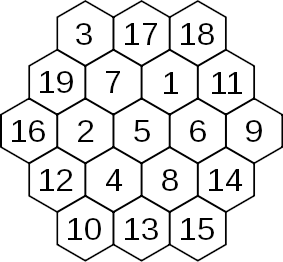
There’s only one normal magic hexagon — only one hexagonal arrangement of cells like the one shown here that can be filled with the consecutive integers 1 to n such that every row, in all three directions, sums to the same total. (This excludes the trivial example of a single cell on its own, as well as rotations and reflections of the hexagon shown here.)
Amazingly, it appears that this lonely example may not have been discovered until 1888! In a 1988 letter to the Mathematical Gazette, Martin Gardner reported that the magic hexagon was given as a problem in the German magazine Zeitschrift für mathematischen und naturwissenschaftlichen Unterricht (Volume 19, page 429) in 1888. The proposer was identified only as von Haselberg, of Stralsund; his solution was published in the next volume.
Gardner writes, “The structure could easily have been discovered by mathematicians in ancient times, but as of now, this is the earliest known publication.”
(Martin Gardner, “The History of the Magic Hexagon,” Mathematical Gazette 72:460 [June 1988], 133.)
In Ulysses, Leopold Bloom’s locked private drawer at 7 Eccles Street contains, among other things:
3 typewritten letters, addressee, Henry Flower, c/o P.O. Westland Row, addresser, Martha Clifford, c/o P.O. Dolphin’s Barn: the transliterated name and address of the addresser of the 3 letters in reversed alphabetic boustrophedontic punctated quadrilinear cryptogram (vowels suppressed) N. IGS./WI. UU. OX/W. OKS. MH/Y. IM …
This actually works: Quadrilinear means that the cipher is to be set in four lines; reversed alphabetic means that the key is a = z, b = y, etc.; and boustrophedontic is a term from paleography meaning that the writing runs right and left in alternate lines. So the cryptogram and its solution look like this:
N . I G S . m a r t h a W I . U U . O X d r o f f i l c W . O K S . M H d o l p h i n s Y . I M b a r n
Apparently Joyce or Bloom forgot that the last line should run right to left.
(From David Kahn, The Codebreakers, 1967.)
In a 1951 article in the New York Times Magazine, Bertrand Russell laid out “the Ten Commandments that, as a teacher, I should wish to promulgate”:
“The essence of the liberal outlook in the intellectual sphere is a belief that unbiased discussion is a useful thing and that men should be free to question anything if they can support their questioning by solid arguments,” he wrote. “The opposite view, which is maintained by those who cannot be called liberals, is that the truth is already known, and that to question it is necessarily subversive.”
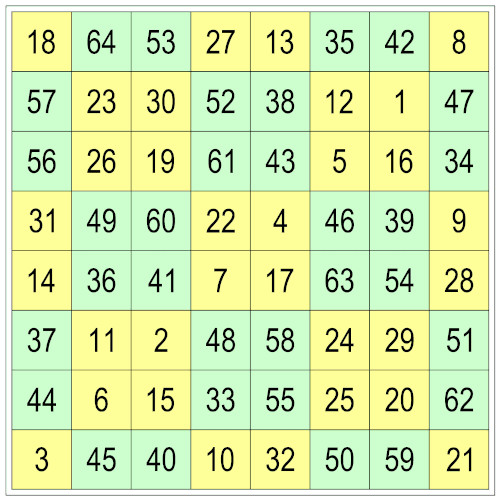
A queen’s tour is the record of a chess queen’s journey around an empty board in which she visits each of the squares once. If the squares are numbered by the order in which she visits them, then the resulting square is magic if the numbers in each rank and file sum to the same total. It’s bimagic if the squares of these numbers also produce a consistent total.
William Walkington has just found the first bimagic queen’s tour, which also appears to be the first bimagic tour of any chess piece. (William Roxby Beverley published the first magic knight’s tour in The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science in 1848.)
Note that here the long diagonals don’t produce the magic sum, as they would in a magic square. This constraint is normally dropped in a magic tour — in fact, of the 140 magic knight tours possible on an 8×8 board, none have two long magic diagonals, and no bimagic queen’s tour with qualifying diagonals is possible on such a board either.
More details, and an interesting description of the search, are on William’s blog. He has been told that a complete list of such bimagic queen’s tours is within reach of a computer search, though the field is daunting — there are more than 1.7 billion essentially different semi-bimagic squares possible on an 8×8 board, and each allows more than 400 million permutations.
In 1882 Anton Chekhov published eight “Questions Posed by a Mad Mathematician.” Here are the first three:
The full list appears in The Undiscovered Chekhov, translated by Peter Constantine (1998). No answers are provided.
At the 1961 Solvay conference on physics, Abdus Salam overheard this conversation between Richard Feynman and Paul Dirac:
Feynman extended his hand towards Dirac and said: ‘I am Feynman.’ It was clear from his tone that it was the first time they were meeting. Dirac extended his hand and said: ‘I am Dirac.’ There was silence, which from Feynman was rather remarkable. Then Feynman, like a schoolboy in the presence of a Master, said to Dirac: ‘It must have felt good to have invented that equation.’ And Dirac said: ‘But that was a long time ago.’ Silence again. To break this, Dirac asked Feynman: ‘What are you yourself working on?’ Feynman said: ‘Meson theories’ and Dirac said: ‘Are you trying to invent a similar equation?’ Feynman said: ‘That would be very difficult.’ And Dirac, in an anxious voice, said: ‘But one must try.’
“At that point the conversation finished because the meeting had started.”
(Abdus Salam, “Physics and the Excellences of the Life It Brings,” in Ideals and Realities: Selected Essays of Abdus Salam, 1987.)
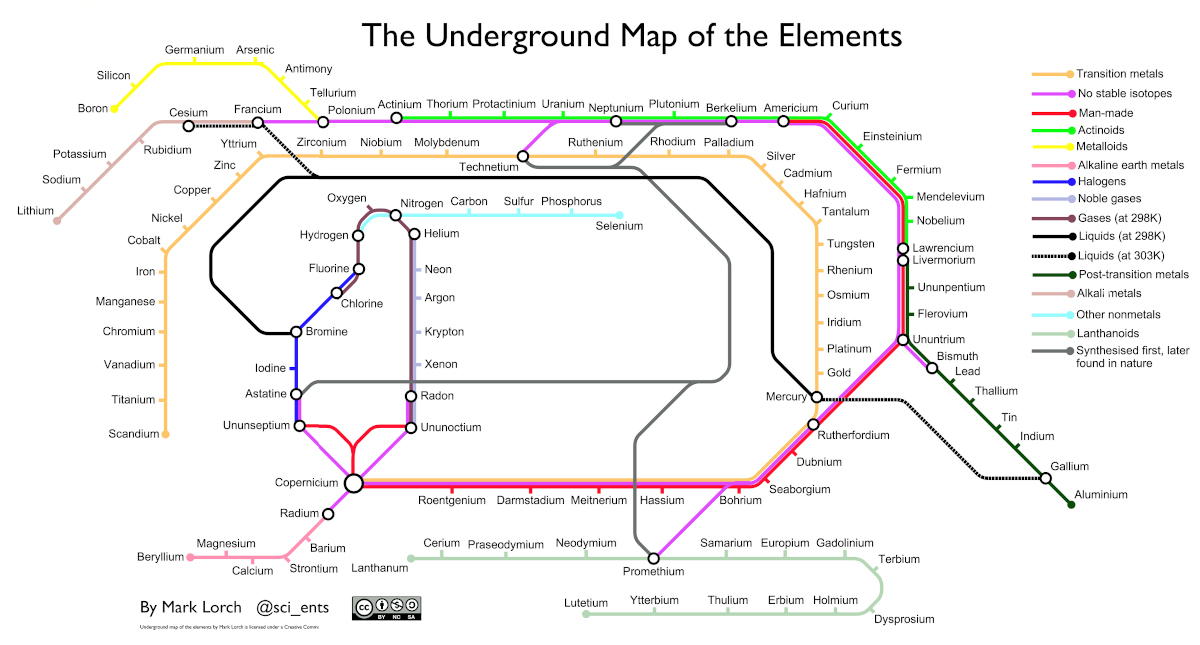
This is brilliant: University of Hull chemist Mark Lorch has combined the periodic table with London’s classic Tube map to create an Underground Map of the Elements.
“My son loves trains. So I came up with a train related twist to an inspection of the periodic table. We sat and cut up a copy of the table and then rearranged each element as a ‘station’ on an underground rail system. Each line represents a characteristic shared by the elements on that line.”
More details at the Guardian and at Chemistry Blog.

“The difference between the amoeba and Einstein is that, although both make use of the method of trial and error elimination, the amoeba dislikes erring while Einstein is intrigued by it.” — Karl Popper, Objective Knowledge: An Evolutionary Approach, 1972
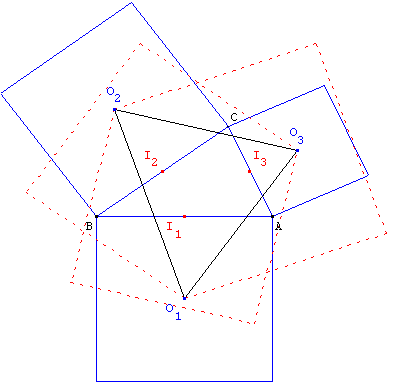
Construct squares outwardly on the sides of triangle ABC, and make a triangle of their centers. Now the centers of squares constructed inwardly on the sides of that triangle will fall on the midpoints of the sides of ABC.
(Due to Luxembourger mathematician Joseph Neuberg, 1840-1926.)